х = -5
Объяснение:
2 - 2(х - 1) = 14
2 - 2х + 2 = 14
-2х + 4 = 14
-2х = 14 - 4
-2х = 10
х = 10/(-2)
х = -(10/2)
х = -5
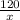часов, а обработал за 
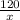часов, закончив работу на 1 час раньше. - =1 (умножим на х(х+20), чтобы избавиться от дробей)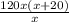
- 
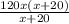=1x(x+20)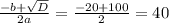
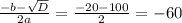- не подходит, поскольку х<0.
2 - 2(х - 1) = 14
2 - 2х + 2 = 14
4 - 2х = 14
2х = 4 - 14
2х = -10
х = -10 : 2
х = -5.