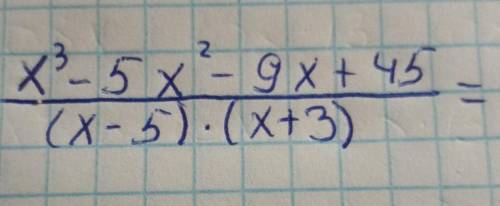
x-3
Объяснение:
issksksksisi
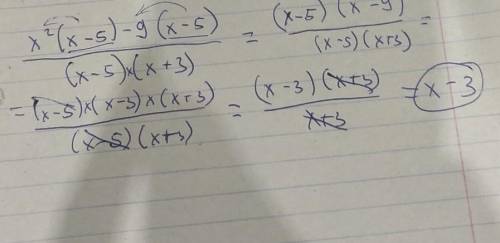
b1+b2+b3=112
b4+b5+b6=14
bn=b1*q^(n-1) - формула n-го члена геометрической прогрессии
=> b2 = b1*q; b3=b1*q^2; b4=b1*q^3; b5=b1*q^4; b6=b1*q^5
b1+b1q+b1q^2=112
b1q^3+b1q^4+b1q^5=14
Вынесем за скобку из первого уравнения b1: b1(1+q+q^2)=112
Вынесем за скобку из второго уравнения b1q^3: b1q^3(1+q+q^2)=14
Выразим из первого уравнения (1+q+q^2): 1+q+q^2=112/b1
Подставим во второе уравнение: b1q^3*(112/b1)=14
q^3*112=14
q^3=1/8
q=1/2
Из первого уравнения: b1=112/(1+q+q^2)=112/(1+1/2+1/4)=112/(7/4)=16*4=64
ответ: 64
b = -5/2
c = 169/16
Объяснение:
y1 = 4x; y2 = -9x
f(x) = x^2 + bx + с
Уравнение касательной в точке (x0; y0):
y(x) = f(x0) + f'(x0)*(x - x0)
В нашем случае точки касания (x1; y1) и (x2; y2) неизвестны
f(x0) = x0^2 + b*x0 + c
f'(x) = 2x + b; f'(x0) = 2x0 + b
y1(x) = x1^2 + b*x1 + c + f'(x1)*(x-x1) = x1^2 + b*x1 + c + (2x1+b)*(x-x1) = x1^2 + b*x1 + c + x(2x1+b) - 2x1^2 - b*x1 = x(2x1+b) + (x1^2 + b*x1 + c - 2x1^2 - b*x1) = 4x + 0
y2(x) = x2^2 + b*x2 + c + f'(x2)*(x-x2) = x2^2 + b*x2 + c + (2x2+b)*(x-x2) = x2^2 + b*x2 + c + x(2x2+b) - 2x2^2 - b*x2 = x(2x2+b) + (x2^2 + b*x2 + c - 2x2^2 - b*x2) = -9x + 0
Составляем систему 4 уравнений:
{ 2x1 + b = 4
{ x1^2 + b*x1 + c - 2x1^2 - b*x1 = 0
{ 2x2 + b = -9
{ x2^2 + b*x2 + c - 2x2^2 - b*x2 = 0
Упрощаем:
{ b = 4 - 2x1
{ c - x1^2 = 0
{ b = -9 - 2x2
{ c - x2^2 = 0
Из 1 и 3 уравнений делаем 1 уравнение, а Из 2 и 4 уравнений делаем 2 уравнение:
{ b = 4 - 2x1 = -9 - 2x2
{ c = x1^2 = x2^2
Из 2 уравнения следует, что: или x2 = x1, или x2 = -x1.
Но из 1 уравнения ясно, что не может быть x2 = x1, потому что 4 не равно -9.
Значит, x2 = -x1, подставляем:
4 - 2x1 = -9 + 2x1
4 + 9 = 2x1 + 2x1
4x1 = 13
x1 = 13/4; x2 = -x1 = -13/4
b = 4 - 2x1 = 4 - 2*13/4 = 4 - 13/2 = -5/2
c = x1^2 = (13/4)^2 = 169/16
x2*(x-5)-9(x-5)
(x-5)*(x+3)
(x-5)*(x2-9)
(x-5)*(x+3)
(x-3)*(x+3)
x+3
= x-3