
Прямые х=1 и у=-2 пересекаются в точке с координатами (1,-2) Это будет точка А.
Прямая х=1 и прямая у=-2х+6 пересекаются в точке с координатами х=1 у=-2*1+6+=4, т.е. (1,4) Это будет точка В.
Прямая у=-2 и прямая у=-2х+6 пересекаются в точке с координатами у=-2, а х находим из уравнения
-2=-2х+6, х=4 Координаты (4,-2) Это будет точка С.
Получился прямоугольный треугольник. Катет АВ - вертикальный его длина разность координат у у точек А и В: 4-(-2)=6, катет АС - горизонтальный, его длина разность координат х у точек А и С: 4-1=3
Площадь треугольника 6*3/2=9
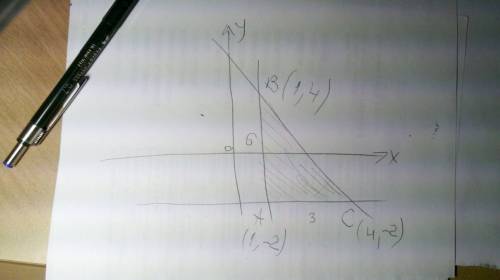
Прямые х=1 и у=-2 пересекаются в точке с координатами (1,-2) Это будет точка А.
Прямая х=1 и прямая у=-2х+6 пересекаются в точке с координатами х=1 у=-2*1+6+=4, т.е. (1,4) Это будет точка В.
Прямая у=-2 и прямая у=-2х+6 пересекаются в точке с координатами у=-2, а х находим из уравнения
-2=-2х+6, х=4 Координаты (4,-2) Это будет точка С.
Получился прямоугольный треугольник. Катет АВ - вертикальный его длина разность координат у у точек А и В: 4-(-2)=6, катет АС - горизонтальный, его длина разность координат х у точек А и С: 4-1=3
Площадь треугольника 6*3/2=9

Диаграмма Венна (также используется название диаграмма Эйлера — Венна) — схематичное изображение всех возможных отношений (объединение, пересечение, разность, симметрическая разность) нескольких (часто — трёх) подмножеств универсального множества. На диаграммах Венна универсальное множество {\displaystyle U} изображается множеством точек некоторого прямоугольника, в котором располагаются в виде кругов или других простых фигур все остальные рассматриваемые множества[1][2].

Диаграмма Венна, показывающая все пересечения греческого, русского и латинского алфавитов (буквы заглавные)
Диаграммы Венна применяются при решении задач вывода логических следствий из посылок, выразимых на языке формул классического исчисления высказываний и классического исчисления одноместных предикатов[3], для :