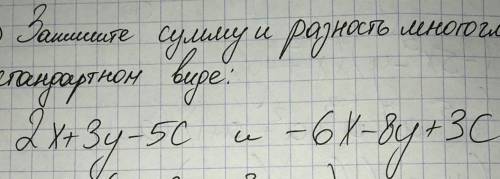
З'ясуємо, як знайти область визначення деяких функцій, заданих формулою.
1. Якщо функція — многочлен, то вона існує при будь-яких значеннях аргумента, тобто її область визначення — всі дійсні числа.
2. Якщо функція задана формулою, яка містить аргумент у знаменнику дробу, то до області визначення функції входять всі дійсні числа, крім тих, які перетворюють знаменник в нуль.
3. Якщо функція задана формулою, яка містить арифметичний квадратний корінь, то до області її визначення входять всі дійсні числа, при яких підкореневий вираз набуває невід'ємних значень.
Область значень функції (множина значень) - усі значення, яких набуває функція.
Функція є парною - якщо для будь-якого х з області визначення функції виконується рівність f(x)=f(-x)
Функція є непарною - якщо для будь-якого х з області визначення функції виконується рівність f(-x)=-f(x)
2х+3х-5с
д= 3^2-4×2×(-5)= 9+40=49
х1= -3+7/2×2= 4/4=1
х2= -3-7/2×2= -10/4= -5/2= -2,5
-6х-8у+3с
д= (-8)^2-4×(-6)×3= 64+72= 136
(целого корня нет из 136, по этому округляем 11,6...≈12)
х1= 8+12/12= 20/12= 10/6= 5/3
х2= 8-12/12= -4/12= -1/3
Объяснение:
д - дискриминант
формула дискриминанта: д= б2-4×а×с
х1= -б+√д/2×а. х2=-б-√д/2×а