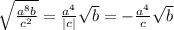
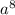из-под корня b не может быть отрицательным, а в первоначальном виде может, при условии, конечно, что a=0. Поэтому ответ такой: если a=0, то выражение равно нулю. Если же a не равно нулю, то выражение может быть преобразовано к указанному виду. А чтобы не было сомнений по поводу отрицательного c, можно поступить так: 
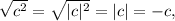так как c отрицательно.
1) раскрываем скобки , в нашем случае перед скобкой стоит цифра 5, значит мы его переумножаем на каждое число в скобке:
5*(-4x)+5*(0.6)+17.5x-0.5 =0
-20x+3+17.5x-0.5=0
2)Теперь визуально или подчеркнув
одинаковые цифры с переменными и без , выполненим действия:
Числа с иксами -20x+17.5x = -2.5x
Обычные числа , без переменных 3-0.5=2.5
Получилось: -2.5x+2.5=0
3) Подставим вместо икса наше условие x=0.8:
-2.5*(0.8)+2.5=-2+2.5=0.5
Т.е наш ответ , при x=0.8 , получается 0.5