Сторона данного треугольника а(3) равна Р:3=6√3:3=2√3 дм
Формула радиуса окружности, описанной около правильного треугольника:
R=a/√3 =>
R=2√3:√3=2 дм
Формула стороны правильного многоугольника через радиус вписанной окружности:
а(n)=2r•tg(180°:n), где r – радиус вписанной окружности, n – число сторон,
Для правильного шестиугольника tg(180°:n)=tg30°=1/√3
a₆=2•2•1/√3=4/√3
P=6•4/√3=8√3 дм
—————
Как вариант: Правильный шестиугольник состоит из 6 равных правильных треугольников.
На рисунке приложения ОН - радиус описанной около правильного треугольника окружности и в то же время высота одного из 6 правильных треугольников, все углы которого 60°; АВ - сторона шестиугольника. Задача решается с т.Пифагора.
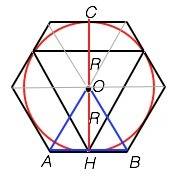
S по течению - 16 км.
t - 3 часа
V течения - 1 км/ч
Составим уравнение.
Пусть Х - скорость в стоячей воде
Значит
Против теч. = х-1
По теч. = х +1
По формуле t = S : V
Состовляем время
Протб теч. = 28 / ( х -1 )
По течен. = 16 / ( х +1 )
Ну а теперь скомпануем.
16/( х+1) + 28 / (х-1) = 3 часа ( это всего времени)
Что бы решить надо найти О.З.
Это ( х-1) ( х+1)
У тройки нет знаменателя поэтому мы должны ему его добавить.
Перепеши тот же пример, и просто добавь 3 × ( х+1) × (х -1 ).
Теперь когда у всех есть О.З, мы можем раскрывать скобки и решать.
16х- 16 +28х +28 = 3х^2 - 3
Иксы в одну сторону, без в другую.
И получим.
3х^2 - 44 х - 15 =0
Д = 529 , из под корня равно 23
Х1 = 15 ( подх.)
х2 = - 1/3 ( неподх.)