
а) 1
б) 1
Объяснение:
Касательной к графику функции у (х) является первая производная у', значение которой в точке x₀ равно тангенсу угла между касательной к графику функции у (х) и осью х.
а)
1) Находим производную:
y' = (х⁶ - 4х)' = (х⁶)' - (4х)' = 5x⁵ -4
2) Находим значение производной y' = 5x⁵- 4 в точке x₀ = 1:
y'(1) = 5x⁵ -4 = 5 · 1⁵ - 4 = 5 - 4 = 1
ответ: 1
б)
1) Находим производную:
y' = (√х - 3)' = (√х)' - (3)' = 1/(2√x) - 0 = 1/(2√x)
2) Находим значение производной y' = 1/(2√x) в точке x₀ = 1/4:
y' (1/4) = 1/(2√x) = 1/ (2 · 1/2) = 1/1 = 1
ответ: 1
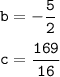
Объяснение:
Даны касательные y₁ = 4·x и y₂ = -9·x к графику функции f(x)=x²+b·x+c.
Пусть прямая y₁ касается к графику функции f(x) в точке x₁, а прямая y₂ касается к графику функции f(x) в точке x₂, то есть:
f(x₁) = y₁(x₁), f'(x₁) = y₁'(x₁) , f(x₂) = y₂(x₂), f'(x₂) = y₂'(x₂) (1).
Так как y₁' = (4·x)' = 4, y₂' = (-9·x) = -9 и f'(x) = (x²+b·x+c)'=2·x+b, то подставляя в уравнения (1) получим 4 уравнения:
x₁²+b·x₁+c = 4·x₁ (2)
2·x₁+b = 4 (3)
x₂²+b·x₂+c = -9·x₂ (4)
2·x₂+b = -9 (5)
Из (3) получим x₁ = (4-b)/2 и подставим в (2):
((4-b)/2)²+b·((4-b)/2)+c = 4·(4-b)/2 или
4-2·b+b²/4+2·b-b²/2+с=8-2·b.
Упростив последнее равенство и получим:
c=4+b²/4-2·b. (6)
Из (5) получим x₂ = (-9-b)/2 и подставим в (4):
((-9-b)/2)²+b·((-9-b)/2)+c = -9·(-9-b)/2 или
81/4+9·b/2+b²/4-9·b/2-b²/2+с=81/2+9·b/2.
Упростив последнее равенство и получим:
c=81/4+b²/4+9·b/2. (7)
Приравниваем выражения (6) и (7):
4+b²/4-2·b = 81/4+b²/4+9·b/2 или
13·b/2 = 4-81/4.
Отсюда
b = (-65/4):(13/2) = -5/2.
Подставим последнее в (6):
c= 4+(-5/2)²/4-2·(-5/2) = 4+25/16+5 = 9+25/16 = 169/16.
Объяснение:
4<a<7 и 3<b<5
1) a+b => 4+3<a+b<7+5 => 7<a+b<12;
3) ab => 4*3 <ab<7*5 => 12<ab<35;
5) 2a+7b => 2*4+7*3<2a+7b<2*7+7*5 => 29<2a+7b< 49;
7) 4b/9a => 4*3/9*4<4b/9a<4*5/9*7 => 1/3<4b/9a<20/63.
или
4*3<4b<4*5 => 12<4b<20;
9*4<9a<9*7 => 36<9a<63;
12/36<4b/9a<20.
Всё верно!!