Составим уравнение касательной к графику функции в точке :
Уравнение касательной:
Преобразуем уравнение:
Так как касательная параллельная прямой , то угловые коэффициенты этих прямых равны:
Проверим, какие касательные получаются в каждом из двух случаев.
При :
Касательная параллельная заданной по условию прямой .
Заметим, что в этом случае касательная совпадает с заданной по условию прямой . Значит, .
Таким образом, условию удовлетворяет единственное значение .
ответ: -1
Составим уравнение касательной к графику функции в точке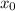 :
:
Уравнение касательной:
Преобразуем уравнение:
Так как касательная параллельная прямой , то угловые коэффициенты этих прямых равны:
, то угловые коэффициенты этих прямых равны:
Проверим, какие касательные получаются в каждом из двух случаев.
При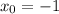 :
:
Касательная параллельная заданной по условию прямой .
.
При :
:
Заметим, что в этом случае касательная совпадает с заданной по условию прямой . Значит,
. Значит, 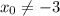 .
.
Таким образом, условию удовлетворяет единственное значение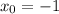 .
.
ответ: -1