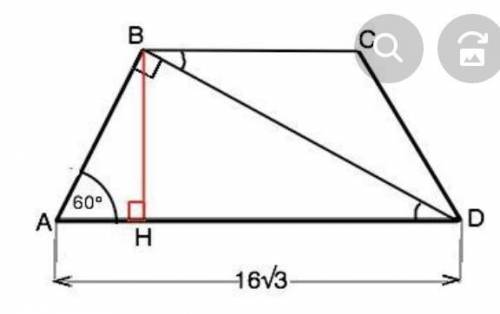
Обозначим трапецию АВСD, AB=CD, АD=16√3, ∠BAD=60°. ∠ABD=90°. Треугольник АВD- прямоугольный, ⇒ ∠АDB=180°-90°-60°=30°. Сторона АВ противолежит углу 30° и равна половине AD. АВ=8√3. Опустим высоту ВН на большее основание. Треугольник АВН - прямоугольный, ∠ АВН=180°-90°-60°=30°. Катет АН=АВ:2=4√3. ⇒ DH=AD-AH=16√3-4√3=12√3. Высота ВН=АВ•sin60°=8√3•(√3/2)=12. Высота равнобедренной трапеции, проведенная из тупого угла, дели основание на отрезки, больший из которых равен полусумме оснований, меньший - их полуразности⇒ DH=(AD+BC):2. Площадь трапеции равна произведению высоты на полусумму оснований. S(ABCD)=BH•DH=12•12√3=144√3 (ед. площади)
==========
Как вариант решения можно доказать, что треугольник DCB - равнобедренный, ВС=CD=AB, вычислить длину высоты и затем площадь ABCD.
см, тогда второй катет - 
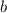см. Площадь прямоугольного треугольника равна 
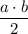, что составляет 210 см² или перепишем сразу 
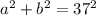
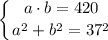
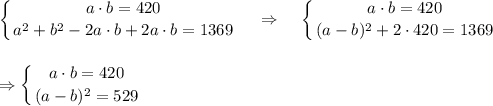
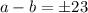. Тогда имеем несколько случаев.
, то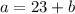 
и подставим в первое уравнение.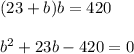
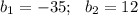см и корень 
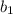не удовлетворяет заданному условию
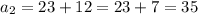см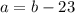
,то подставив в первое уравнение, получим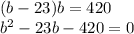
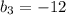
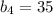см и корень 
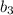не удовлетворяет условию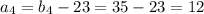
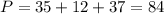см
