В решении.
Объяснение:
№2 Яке найбільше натуральне значення х задовольняє нерівність 18-3(х-15)>11x
N°3. Яке найменше ціле значення а задовольняє нерівність: а² + 4a < (a + 2)²
№2 Какое наибольшее натуральное значение х удовлетворяет неравенству 18-3(х-15)>11x?
18 - 3(х-15) > 11x
18 - 3х + 45 > 11x
63 - 3x > 11x
-3x - 11x > -63
-14x > -63
14x < 63 знак меняется при делении и умножении на -1;
х < 4,5
Решение неравенства: х∈(-∞; 4,5).
Наибольшее целое значение: х = 4.
№3. Какое наименьшее целое значение а удовлетворяет неравенству: а² + 4a < (a + 2)²?
а² + 4a < (a + 2)²
а² + 4а < a² + 4a + 4
а² + 4а - a² - 4a - 4 < 0
-4 < 0
Решение неравенства: x ∈ R (х может быть любым).
Не существует наименьшего целого значения а, которое удовлетворяет данному неравенству.
Объяснение:
Дано: F(x) = 0,5*x² + (2)*x + (4), y(x)=1*x+8
Найти: S=? - площадь фигуры
Пошаговое объяснение:
1) Находим точки пересечения графиков: F(x)=y(x).
-0,5*x²+-1*x+4=0 - квадратное уравнение
b = 2 - верхний предел, a = -4 - нижний предел.
2) Площадь - интеграл разности функций. Прямая выше параболы.
s(x) = y(x) - F(x) = 4 - x - 0,5*x² - подинтегральная функция
3) Интегрируем функцию и получаем:
S(x) = lim(8-x - 4-2*x+x)*dx = 4*x + (-1)/2*x² + (-0,5)/3*x³
4) Вычисляем на границах интегрирования.
S(b) = S(2) = 8 -2 - 1,33 = 4,67
S(a) = S(-4) = -16 + -8 + 10,67 = -13,33
S = S(-4)- S(2) = 18(ед.²) - площадь - ответ
Задача Б. y = 1/8*x², y = 1/2*(x+8).
Находим точки пересечения графиков.
Дано: F(x) = 0,125*x², y(x)= 0,5*x+4
Найти: S=? - площадь фигуры
Пошаговое объяснение:
1) Находим точки пересечения графиков: F(x)=y(x).
0,125*x² - 0,5*x - 4=0 - квадратное уравнение
b = 8 - верхний предел, a = -4 - нижний предел.
2) Площадь - интеграл разности функций. Прямая выше параболы.
s(x) = y(x) - F(x) = -4 - 0,5*x + 0,125*x² - подинтегральная функция
3) Интегрируем функцию и получаем:
S(x) = -4*x - 0,5/2*x² + 0,125/3*x³
4) Вычисляем на границах интегрирования.
S(а) = S(-4) = 16 - 4 -2,67 = 9,33
S(b) = S(8) = -32 -16 + 21,33 = -26,67
S = S(8)- S(-4) = 36(ед.²) - площадь - ответ
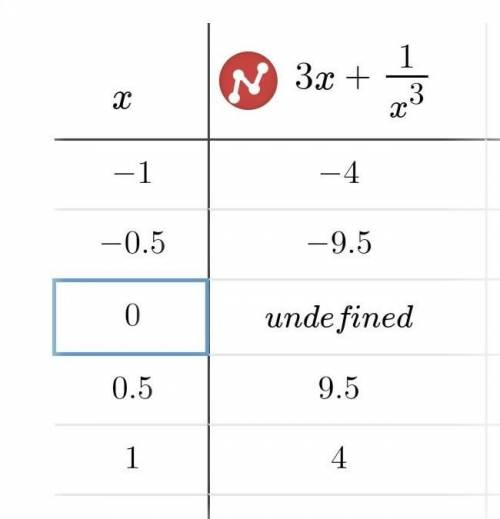
1) Нет пересечений с осью x
1) Нет пересечений с осью x2) Нет пересечений с осью y
1) Нет пересечений с осью x2) Нет пересечений с осью y3)(область определения) x принадлежит R
1) Нет пересечений с осью x2) Нет пересечений с осью y3)(область определения) x принадлежит R4)(производная) y'= 3-3/x^4
1) Нет пересечений с осью x2) Нет пересечений с осью y3)(область определения) x принадлежит R4)(производная) y'= 3-3/x^45) Нет горизонтальных асимптот
1) Нет пересечений с осью x2) Нет пересечений с осью y3)(область определения) x принадлежит R4)(производная) y'= 3-3/x^45) Нет горизонтальных асимптот6) (Наклреная асимптота) y=3x
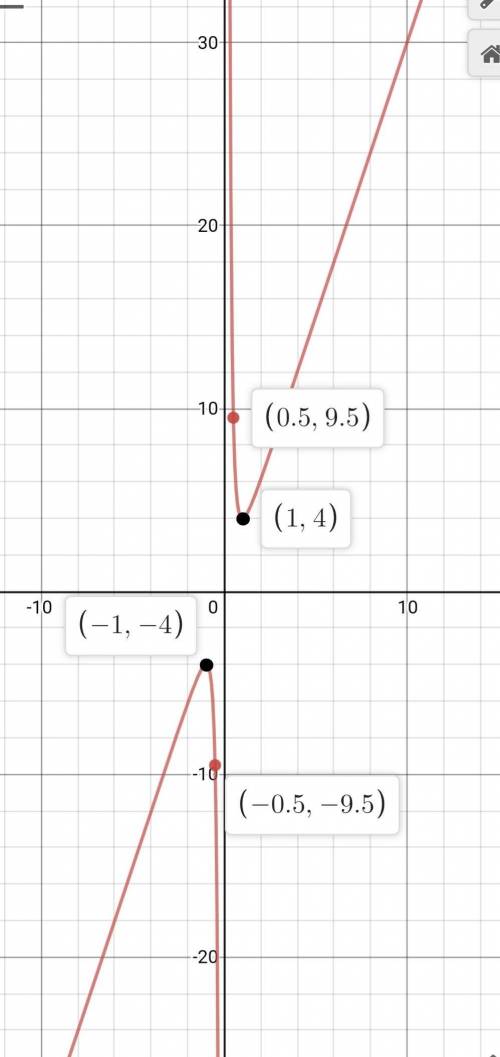
Таблица для построения графика, и сам график в закрепе)
№2 - 4 (х<9/2)=(х<4,5)
№3 - 4 (0<4)