ответ: 10,6
Объяснение:
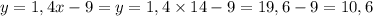
Б. (х+у)·у
Объяснение:
Перевод: Натуральные числа x и y такие, что x - чётное, y-- нечётное. Значение которого по представлению выражений не является четным числом?
Нужно знать:
а) сумма двух нечётных чисел будет чётной;
б) сумма чётного числа с нечётным числом будет нечётной;
в) произведение нечётного числа с нечётным числом будет нечётным;
г) произведение чётного числа с нечётным числом будет чётным.
А. у² + 7 = y·y + 7 --> нечётное · нечётное + нечётное => чётное;
Б. (х+у)·у - (чётное + нечётное) · нечётное => нечётное;
В. х·(х+у) - чётное · (чётное + нечётное) => чётное;
Г. х·(х²+у²) - чётное·(чётное · чётное + нечётное · нечётное) => чётное;
Д. х·(у+1)/2 - чётное·(нечётное+1)/2 = чётное/2· чётное => чётное.
Объяснение:
Дано: ∆ABC, в котором ∠C = 90º.
Доказать: a2 + b2 = c2.
Пошаговое доказательство:
Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:
∠ACB =∠CHA = 90º,
∠A — общий.
Также прямоугольная фигура ∆CBH подобна ∆ABC:
∠ACB =∠CHB = 90º,
∠B — общий.
Введем новые обозначения: BC = a, AC = b, AB = c.
Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.
Значит a2 = c * HB, b2 = c * AH.
Сложим полученные равенства:
a2 + b2 = c * HB + c * AH
a2 + b2 = c * (HB + AH)
a2 + b2 = c * AB
a2 + b2 = c * c
a2 + b2 = c2
Теорема доказана.
Объяснение:
y=1,4x-9=y=1,4*14-9=19,6-9=10.6