1. Находим х из 1-го уравнения: х=5+у.
Найденный x подставляем во 2-е уравнение:
(5+у)^2 - 15у=109
25+10у+у^2 -15 у-109=0
у^2-5у-84=0
D=25+336=361
x=(5+-19)/2
x=12, тогда y=7
x=-7, тогда y=-12
ответ: (12;7) и (-7;-12)
2.
x+y=14
x*y=-72
x=14-у
(14-у)у=-72
14у-у^2+72=0
у^2-14у-72=0
D=196-4*1*(-72)=196+288=22^2
у1=14-22/2=-8/2=-4
y2=14+22/2=36/2=18
x1=14+4=18
x2=14-18=-4
ответ: -4 и 18
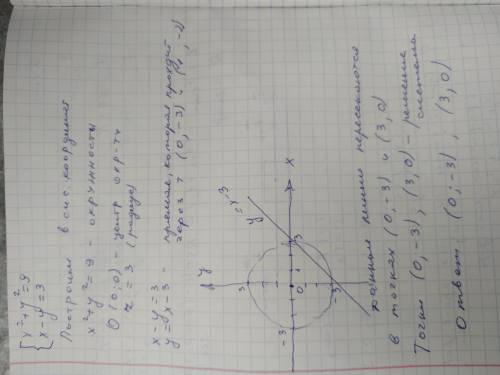
3. Решение в прикрепленном файле:
ответ: (0;-3) (3;0)
4. y=1 / 2 x2 и прямой y=3x-4
1/2x2=3x-4
x2-6x+8=0
D=36-32=4
x12=(6+-2)/2=4 2
x=4
y=8
x=2
y=2
Объяснение:
Для того, чтобы представить выражение (x - y)(x + y) в виде многочлена стандартного вида мы можем действовать двумя .
Первый .
Выполним умножение скобки на скобки, а затем выполним приведение подобных слагаемых.
Открываем скобки и получаем:
(x - y)(x + y) = x * x + x * y - x * y - y * y = x2 + xy - xy - y2.
Приведем подобные и получим:
x2 + xy - xy - y2 = x2 - y2.
Второй .
Применим формулу сокращенного умножения разность квадратов (a - b)(a + b) = a2 - b2.и получим:
(x - y)(x + y) = x2 - y2.