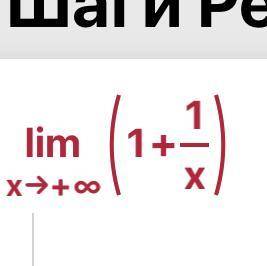
Сначала найду саму формулу, задающую обратную функцию. Для этого заменю в исходной функции x на y и наоборот, а затем выражу y через x:
x = -1/y
y = -1/x
Значит. данная функция на своей области определения обратна сама себе. Теперь надо просто построить одну исходную функцию. Это гипербола, состоящая из двух ветвей, лежащих во 2 и 4 координатных четвертях. Просчитаю точки:
x 1 2 4 5 -1 -2 4
y -1 -0.5 -0.25 -0.2 1 0.5 0.2
Отметь теперь эти точки на координатной плоскости и соедини их. Задача выполнена.
(x+1)(x^2-x+1)-x(x+3)(x-3) Упростим данное выражение, для этого раскроем скобки. Также заметим, что (x+1)(x^2-x+1) - это формула сокращенного умножения: a³+b³=(a+b)(a²-ab+b²) , где, в нашем случае, a - это x, а b - это x, таким образом, (x+1)(x^2-x+1)=x³+1.
Заметим, (x+3)(x-3) - тоже формула сокращенного умножения - разность квадратов
(x+3)(x-3)=x²-9/ Преобразуем наше выражение, дораскрываем скобки:
(x+1)(x^2-x+1)-x(x+3)(x-3)=x³+1-x(x²-9)=x³+1-x³+9x=9x+1.
Найдем значение выражение при x=1:
9*1+1=10.
Удачи!
ответ: 1 .
Объяснение:
lim ( 1 + 1/x ) = lim 1 + lim ( 1/x ) = 1 + 1/( +∞ ) = 1 + 0 = 1 .
x-->+∞ x-->+∞ x-->+∞