![Випадкова величина X розподілена рівномірно в діапазоні [A;B]. Знайти її функції щільності та розпод](/tpl/images/4678/9924/e7b0c.jpg)
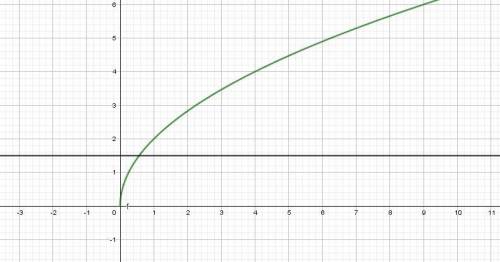
1) Построим графики функций  и прямую параллельную оси ОХ
и прямую параллельную оси ОХ 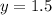
Графики пересекаются в точке (0.5625; 1.5), где x = 0.5625 - корень данного уравнения
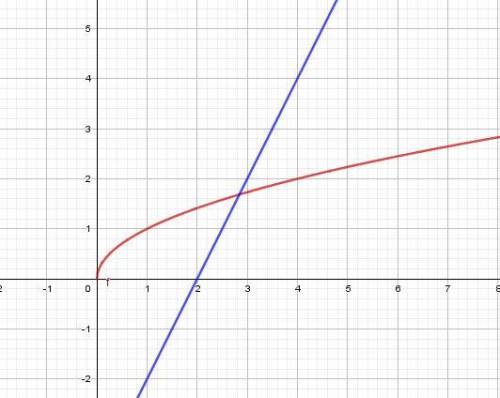
2) Построим график функции 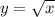 и прямую
и прямую 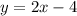 проходящую через точки (0;-4), (2;0). Отсюда абсцисса точки пересечения двух графиков
проходящую через точки (0;-4), (2;0). Отсюда абсцисса точки пересечения двух графиков 
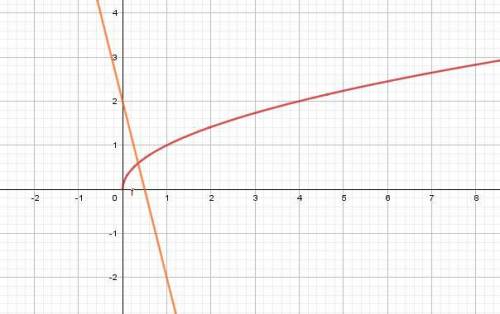
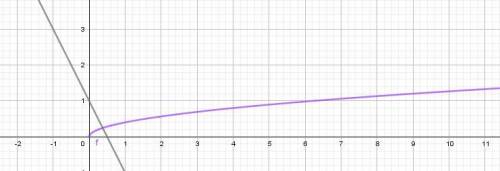
3) Построим график функции y = √x и прямую y = 2 - 4x, проходящую через точки (0;2), (1;-2). Абсцисса точки пересечения двух графиков равна 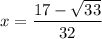
4) Построим график функции y = 0.4√x и прямую y = 1 - 2x, проходящую через точки (0;1), (1;-1). Абсцисса точки пересечения двух графиков равна 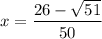
1)Решение системы уравнений (2; 3);
2) а)Координаты точки пересечения прямых (2; -2)
Решение системы уравнений (2; -2)
2) б)Прямые параллельны.
Система уравнений не имеет решения.
3)а= -1; b=7.
Объяснение:
1. Какая из пар чисел (-5;1); (1;4); (2;3) является решением системы уравнений:
2х-7у= -17
5х+у=13
Решить систему уравнений.
Выразим у через х во втором уравнении, подставим выражение в первое уравнение и вычислим х:
у=13-5х
2х-7(13-5х)= -17
2х-91+35х= -17
37х= -17+91
37х=74
х=74/37
х=2
у=13-5х
у=13-5*2
у=3
Решение системы уравнений (2; 3)
2. Решить графическим систему уравнений:
а) у+х=0
4х+у=6
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
у+х=0 4х+у=6
у= -х у=6-4х
Таблицы:
х -1 0 1 х -1 0 1
у 1 0 -1 у 10 6 2
Согласно графика, координаты точки пересечения прямых (2; -2)
Решение системы уравнений (2; -2)
б)х+у= -1
3х+3у= -2
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
х+у= -1 3х+3у= -2
у= -1-х 3у= -2-3х
у=(-2-3х)/3
Таблицы:
х -1 0 1 х -1 0 1
у 0 -1 -2 у 0,33 -0,67 -1,67
Согласно графика, прямые параллельны.
Система уравнений не имеет решения.
3.Пара чисел (3;-2) является решением системы уравнений
2х+ау=8
bх+3у=15
Найдите значения а и b.
Подставим известные значения х и у (решение системы) в уравнения:
2*3+а*(-2)=8
b*3+3*(-2)=15
Выполняем необходимые действия:
6-2а=8
3b-6=15
Из уравнений вычисляем а и b:
-2а=8-6
-2а=2
а=2/-2
а= -1
3b=15+6
3b=21
b=21/3
b=7