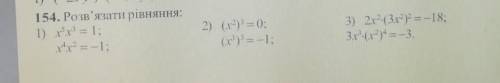
Катя, смотрите.. . Студент посетит следующую библиотеку только в том случае, если необходимой ему книги в предыдущей библиотеке не имелось.
Случайная величина Х- число посещенных библиотек - может принимать следующие значения:
Х1=1
Х2=2
Х3=3
Х4=4
Для того, чтобы найти вероятности этих значений, обозначим
p=0.3 - вероятность того, что студент получил нужную книгу
q=0.7 - вероятность того, что студент не получил нужную книгу
Тогда :
Р (Х=1)=0,3 (книга сразу получена в первой библиотеке)
Р (Х=2)=0,7*0,3=0,21 (в первой библиотеке книги не было, во второй есть)
Р (Х=3)=0,7*0,7*0,3=0,147 (в первых двух библиотеках книги не было, в третьей есть)
Р (Х=4)=0,7*0,7*0,7=0,343 (в первых трех библиотеках книги не было)
Проверяем: сумма вероятностей должна быть равна 1.
0,3+0,21+0,147+0,343=1 - верно
Объяснение:
Наверно так!
Если одночлены состоят из одинаковых переменных в одинаковых степенях, то они являютсяподобными. Коэффициенты одночленов при этом могут различаться. Примеры подобных одночленов:
3a2 и –4a2; 31 и 45; a2bx4 и 1,4a2bx4; 100y3и 100y3
Но одночлены –6ab2 и 6ab не являются подобными, так как у них переменная b находится в разных степенях.
Подобные одночлены обладают удивительным свойством — их можно легко складывать и вычитать. Если нужно найти сумму двух или более подобных одночленов, то их коэффициенты надо сложить, а переменные в сумме оставить без изменений. Если же требуется найти разность двух подобных одночленов, то коэффициент одного одночлена надо вычесть из второго, а переменные оставить без изменений. Примеры:
4x2 + 15x2 = 19x2
5ab – 1,7ab = 3,3ab
13a10b5c3 – 13a10b5c3 = 0a10b5c3 = 0
Эти действия называются приведением подобных одночленов.
Почему же подобные одночлены можно так складывать и вычитать? Попробуем упростить выражения, не используя правила приведения подобных одночленов:
2x + 4x = (x + x) + (x + x + x + x) = x + x + x + x + x + x = 6 * x = 6x
2x – 4x = (x + x) – (x + x + x + x) = x + x – x – x – x – x = – x – x = – (x + x) = –(2x) = –2x
То есть свойство подобных членов вытекает из правила арифметики о том, что произведение двух чисел является ничем иным как суммой из слагаемых одного числа, где количество слагаемых равно другому числу:
2 * 3 = 3 + 3 = 2 + 2 + 2
1) Х1=1, Х2=-1 ; Х≠0
2) X=0, X=-1
3)X≠0, X=-1