РЕБЯТА С ТЕСТОМ. Уравнение x2+3x−4=0 является:

приведённым
неприведённым

Дано уравнение 15x2+39x−11=0.
Запиши старший коэффициент, второй коэффициент и свободный член.

Старший коэффициент-
.
Второй коэффициент-
.
Свободный член-

Найди корни неполного квадратного уравнения 2x2−8=0.

(Сначала вводи больший корень.)

x=
x=

Реши неполное квадратное уравнение 5x2−15x=0

(первым вводи меньший корень).
Корни равны
x=

x=

Найди дискриминант квадратного уравнения 2x2+8x+6=0.

ответ: D=

Реши уравнение x2+24x−5=0.

Нет верного ответа
x1=0;x2=1
x1=−12+149−−−√;x2=0
x1=−12+149−−−√;x2=−12−149−−−√

Найди корни квадратного уравнения x2+6x+9=0

(первым вводи больший корень; если корни одинаковые, впиши одинаковые числа в оба окошка).

x1 =
x2 =

При каких значениях x верно равенство x2−8=28x?

ответ: x1,2=
±√=

👇

Открыть все ответы

Ответ:

Olzhas2889

28.09.2022

Упростить выражение:

$\left(\frac{6}{y^2-9}+\frac{1}{3-y}\right)\cdot \frac{y^2+6y+9}{5} = \\\\= \left(\frac{6}{(y-3)(y+3)}-\frac{1}{y-3}\right)\cdot \frac{(y+3)^2}{5} = \\\\= \frac{6-y-3}{(y-3)(y+3)} \cdot \frac{(y+3)^2}{5} = \\\\= -\frac{(y-3)(y+3)^2}{5(y-3)(y+3)} = \\\\=-\frac{y+3}{5}$

Задача: Два автомобиля выезжают одновременно из одного города в другой, находящийся на расстоянии 560 км. Скорость первого на 10 км больше скорости второго, и поэтому первый автомобиль приезжает на место на 1 час раньше другого. Определить скорость каждого автомобиля.

Пусть скорость второго автомобиля — х км/ч, тогда скорость первого — х+10 км/ч. Второй был в пути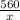 $\frac{560}{x}$ часов, а первый — 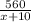$\frac{560}{x+10}$ часов. Зная, что второй автомобиль был в дороге дольше на 1 час, составим и решим математическую модель:

$\frac{560}{x} - \frac{560}{x+10} = 1\\560(x+10)-560x=x(x+10)\\560x+5600-560x=x^2+10x\\x^2+10x-5600=0\\\frac{D}{4}=25+5600=5625=75^2 \\x=-5\pm \sqrt{75^2} = \\x_1 = -5+75=70\\x_2 = -5-75=-80 \:\: \Rightarrow \:\: x_2 \leq 0 \:\: \Rightarrow\:\: x_2 \in \varnothing$

Скорость второго автомобиля — х = 70 км/ч, скорость первого — х+10 = 70+10 = 80 км/ч

скорость первого автомобиля — 80 км/ч;скорость второго автомобиля — 70 км/ч.

Задача: При каких значения x функция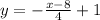 $y=-\frac{x-8}{4}+1$ принимает положительные значения.

$-\frac{x-8}{4}+10 \:\: \big | \cdot (-4) \\-\frac{-4(x-8)}{4} +(-4)0\cdot(-4) \\x-8-4$

$x\in (-\infty; 12).$

ответ: x < 12 или x ∈ (−∞; 12).

4,8(27 оценок)

Ответ:

mokovanins

28.09.2022

1) Смотри на картинке у=-2х+1
a)наименьшее и наибольшее значение функции на отрезке[-1;2]
наибольшее - при х=-1 у=-2*(-1)+1=2+1=3
наименьшее - при х=2 у=-2*2+1=-4+1=-3
b)обозначите переменной х,при которых графич.функций расположены на оси Ох
это х=0,5
2)Найдите координаты точки пересечения y=3-x,y=2x
Решим систему уравнений:
$\left \{ {{y=3-x} \atop {y=2x}} \right. ,3-x=2x, 3x=3, x=1, y=2$
3)a)Задайте линейную функцию y=kx,если известно,что ее график параллелен прямой -3x+y-4=0
y=3x
b)Определите,возрастает или убывает заданная вами линейная функция
возрастает, т.к. k>0
Решите,. 1)постройте график линейной функции y=-2x+1 c графика найдите: a)наименьшее и наибольшее зн