Даны векторы x={-1, 7, 0}, p={0, 3, 1}, q={1, - 1, 2}, z={2, - 1, 0}.
Разложение вектора имеет вид: x = αp + βq + γz.
Из равенства векторов следует равенство их одноимённых координат.
Из этого следует система линейных уравнений:
{αp1 + βq1 + γz1 = -1,
{αp2 + βq2 + γz2 = 7,
{αp3 + βq3 + γz3 = 0.
Решение системы методом Крамера (по треугольной схеме).
Найдём основной определитель системы .
0 1 2 | 0 1
3 -1 -1 | 3 -1
1 2 0 | 1 2.
D = 0 -1 + 12 -0 -0 + 2 = 13.
Заменяем 1-й столбец на вектор результатов B:
-1 1 2 | -1 1
7 -1 -1 | 7 -1
0 2 0 | 0 2.
D1 = 0 + 0 + 28 - 0 - 2 - 0 = 26.
Заменяем 2-й столбец на вектор результатов B:
0 -1 2 | 0 -1
3 7 -1 | 3 7
1 0 0 | 1 0.
D2 = 0 + 1 + 0 - 0 - 0 - 14 = -13.
Заменяем 3-й столбец на вектор результатов B:
0 1 -1 | 0 1
3 -1 7 | 3 -1
1 2 0 | 1 2.
D3 = 0 + 7 - 6 - 0 - 0 - 1 = 0.
α = 26/13 = 2.
β = -13/13 = -1.
γ = 0/13 = 0.
Получили разложение x = 2p - q.
а)
Всего выбирать мы можем из 9+8=17 человек. Число которыми можно выбрать 7 человек из 17, равно числу сочетаний из 17 по 7:
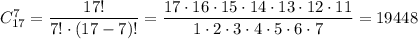
б)
Варианты, которые допустимы в таком случае:
- в бригаде 3 маляра и 4 штукатура
- в бригаде 4 маляра и 3 штукатура
- в бригаде 5 маляров и 2 штукатура
- в бригаде 6 маляров и 1 штукатур
- в бригаде 7 маляров
Например, для первого варианта:
- 3 маляра выбираются из 9 человек, поэтому число выбрать маляров равно числу сочетаний из 9 по 3
- 4 штукатура выбираются из 8 человек, поэтому число выбрать штукатуров равно числу сочетаний из 8 по 4
- выбор маляров и штукатуров независим, поэтому полученные количества нужно перемножить
Рассуждая так для каждого варианта, получим:
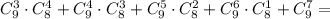
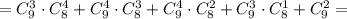
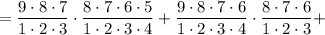
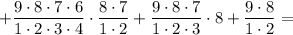

в)
Вероятность того, что в бригаде будет не менее 3 маляров, равна отношению числа которыми можно укомплектовать бригаду при условии, что в ней будет не менее 3 маляров, к общему числу укомплектовать бригаду.
Обе нужные величины уже найдены, поэтому получим:
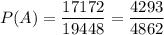
Объяснение: ( ^ -знак степени, V -корень)
a лежит во 2-й четверти, значит, cos, tg, ctg <0
cos^2 x=1-sin^2 x=1-(V2 /2)^2=1-1/2=1/2, cosx=-V2/2,
tgx=V2/2 :(-V2 /2)=-1, ctga=-1