Добрый день! Рад стать вашим учителем и помочь вам разобраться в данной задаче.
Чтобы найти первообразную функции f(x), нам необходимо найти такую функцию F(x), производная которой равна данной функции f(x). То есть, если мы возьмем производную от F(x), то получим f(x).
Для начала, найдем производную от f(x). Возьмем производную от каждого члена функции по отдельности:
Теперь, чтобы найти функцию F(x), чья производная равна f(x), мы должны интегрировать данную производную. То есть, нам нужно найти такую функцию F(x), производная которой будет равна 12x^2 - 2.
Итак, мы получили первообразную функции f(x): F(x) = 4x^3 + 12C1 - 2x - 2C2.
Также, в условии дано, что график функции проходит через точку м(1; -2). Чтобы удовлетворить это условие, мы можем использовать данную точку для определения значений произвольных постоянных C1 и C2.
Подставим значения x = 1 и y = -2 в наше уравнение:
Теперь у нас есть уравнение, которое содержит две неизвестные: С1 и С2. Чтобы получить значения этих постоянных, нам нужна еще одна точка, через которую проходит график функции. Если у вас есть такая точка, пожалуйста, предоставьте ее для дальнейших вычислений.
а) Чтобы привести многочлены к стандартному виду, нужно сложить или вычесть одночлены с одинаковыми переменными и степенями, исключая возможные повторения.
Для первого многочлена (2aa^2 3b+a8b) мы видим два одночлена - 2aa^2 3b и a8b. Оба содержат переменные a и b, поэтому мы можем сложить их вместе. Сначала сложим коэффициенты для одинаковых переменных:
2 + 1 = 3 (коэффициенты при a)
a^2 и a не являются одинаковыми переменными, поэтому мы оставляем их как есть.
3 + 8 = 11 (коэффициенты при b)
Таким образом, первый многочлен можно привести к стандартному виду: 3a^2b + 11ab.
б) Во втором многочлене (8x 3y (-5y)-7x^2 4y) мы также видим два одночлена - 8x и (-7x^2 4y). Оба содержат переменные x и y, поэтому мы можем сложить их вместе. Сначала сложим коэффициенты для одинаковых переменных:
8 + (-7) = 1 (коэффициенты при x)
3y и (-5y) не являются одинаковыми переменными, поэтому мы оставляем их как есть.
1 + 4 = 5 (коэффициенты при y)
Таким образом, второй многочлен можно привести к стандартному виду: x + 3y - 5y - 7x^2 + 4y = -7x^2 + x + 2y.
в) Третий многочлен (20xy+5yx-17xy) содержит три одночлена - 20xy, 5yx и (-17xy). Единственной разницей между ними является порядок переменных x и y, но это не влияет на сумму. Мы можем сложить коэффициенты для одинаковых переменных:
20 + (-17) = 3 (коэффициенты при xy)
3 (коэффициенты при xy) - результат суммирования всех одночленов без повторений переменных.
Таким образом, третий многочлен можно привести к стандартному виду: 3xy.
г) В четвертом многочлене (8ab^2-3ab^2-7ab^2) мы видим три одночлена - 8ab^2, -3ab^2 и -7ab^2. Все они содержат переменные a и b, поэтому мы можем сложить их вместе. Сначала сложим коэффициенты для одинаковых переменных:
8 + (-3) + (-7) = -2 (коэффициенты при ab^2)
Таким образом, четвертый многочлен можно привести к стандартному виду: -2ab^2.
Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой, следовательно,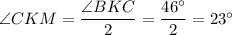
Поскольку KM - высота, проведенная к основанию, то