∉ и И
Объяснение:
Во первых множество всех натуральных чисел обычно обозначают буквой N.
2. Если к натуральным числам присоединить число 0 и все целые отрицательные числа: −1,−2,−3,−4... — то получится множество целых чисел. Это множество обычно обозначают буквой Z.
3. Если к множеству целых чисел присоединить все обыкновенные дроби, то получится множество рациональных чисел. Это множество обычно обозначают буквой Q.
4. ∈ — знак принадлежности (элемент принадлежит множеству).
5. ∉ — элемент не принадлежит множеству.
попробую дать более подробный разбор
итак дано неравентсво
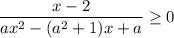 . где a>0
. где a>0
рассмотрим знаменатель дроби
зададим функцию f(x)=ax²-(a²+1)x+a; т.к. a>0 то это парабола, ветви "вверх"
найдем ее корни
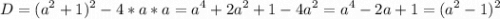
тогда
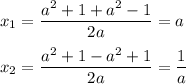
а теперь рассуждения:
чтобы решить неравентсво методом интервалов определяем корни числителя и знаменателя, это числа 2, a и 1/а
1) все корни различны
напомню что а и 1/а корни параболы "ветви вверх" , х=2 корень прямой направленной тоже вверх. Тогда не проблема расставить знаки промежутков
получим вариант №1
парабола ___+___ 1/а______---_______а___+__
прямая ------- 2 +
и тогда решением будет (1/a;2] ∪ (a;+∞)
увы- не луч.. а отрезок и луч
вариант №2
парабола __+_ 1/а___---__а___+_______
прямая ------- 2 +
и тогда решением будет (1/a;а) ∪ [2;+∞)
увы- не луч.. а отрезок и луч
2) теперь допустим что a=2; тогда 1/a=0.5
рисуем
парабола __+_ 1/а___---__а___+_______
прямая ------- 2 +
и тогда решением будет (1/2;2) ∪ (2;+∞)
т.к. х=2 корень знаменателя и он выкалывается
и опять не луч
аналогично при 1/а=2
3) осталось проверить условие что а=1/а, это возможно при а=1
рисуем
парабола __+_ 1/а=а___+_______
прямая ------- 2 +
и тогда решением будет [2;+∞)
Уряяя. получили просто луч
х1*х2=с =-6 по теореме Виета
х²+5х+6=0
х1,2 =(-5+-√25-24)/2=(-5+-1)/2
х1=-3
х2=-2
2) х1+х2=1/12
х1*х2=-1/12
х²-1/12х+1/12=0
12х²-х-1=0
х1,2=(1+-√1+48)/24=(1+-7)/24
х1=8/24=1/3
х1=1/3
х2=-6/24=-1/4
х2=-1/4