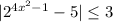
Відповідь:
Пояснення:
2. Исследуем функцию на монотонность и на экстремум:
Критические точки функции:
,
,
Определим знак производной в каждом интервале монотонности:
, точка max, так как производная изменила знак с "+" на "−",
, точка min, так как производная изменила знак с "−" на "+".
Вычислим сам экстремум функции в этих точках:
3. Исследуем функцию на выпуклость, вогнутость кривой и перегиб:
Критические точки: , , ,
Определим знак II производной в интервале кривизны:
, значит, кривая выпуклая на промежутке,
, значит, кривая вогнутая на промежутке;
Вычислим ординату точки перегиба:
4. Найдём дополнительные точки графика:
По результатам исследования строим график функции:
Пример 2. Исследовать функцию по первой и второй производной и построить её график: .
1. Область определения функции ,
точка разрыва, чтобы определить её характер, найдём правосторонний и левосторонний пределы функции в этой точке:
Значит, точка разрыва рода,
прямая вертикальная асимптота графика функции.
Найдём наклонную асимптоту графика:
где угловой коэффициент прямой найдём по формуле
Так как существует, то есть и наклонная асимптота. Вычисляем коэффициент b:
Значит, наклонная асимптота графика имеет уравнение .
2. Исследуем функцию на монотонность и на экстремум:
, учтем правило дифференцирования
Критические точки функции:
, , , , х=2,
5x^-17x-12>0
приравниваем к нулю
D=289-240=49 D>0-2k
x1=(17+7):10=2 целых 2/5
x2=(17-7):10=1
x^-121<0
приравниваем к нулю и решаем
x^=121
x1|2=+-11
x^>4,7x
приравниваем..переносим 4,7х в лево получим это же число с
противоположным знаком.
x^-4,7x=0
выносим х за скобки
x(x-4,7)=0
х=0 или х-4,7=0
х=4,7
x(x-7)-18>7(9-x)
откроем скобки и получим:
х^-7x-18=63-7x
переносим в лево
x^-81=0
x1|2=+-9
(x+9) (x-3) <0
откроем скобки и приравняем к нулю
x^-3x+9x-27=0
x^+6x-27=0
D1=9+27=36
x1=(-3+6)=3
x2=(-3-6)=-9
чертишь плоскость и интервалы в первом интервале будет + а остальные чередуются тоесть...+-+-+...и т.д.
ответ: х∈[-1;-√2/2]∪[√2/2;1]
Объяснение:
неравенство равносильно следующему
-3≤2⁴ˣ²⁻¹-5≤3,
5-3≤2⁴ˣ²⁻¹-5+5≤3+5,
2≤2⁴ˣ²⁻¹≤8
2≤2⁴ˣ²⁻¹≤2³
2¹≤2⁴ˣ²⁻¹≤2³, т.к. функция у=2ˣ возрастающая, то
4х²-1≥1⇒4х²-2≥0 (1)
4х²-1≤3⇒4х²-4≤0 (2)
Решим сначала (1) методом интервалов, х²=1/2;х=±√2/2
-√2/2√2/2
+ - +
х∈(-∞;-√2/2]∪[√2/2;+∞)
решим второе неравенство (2) методом интервалов.
4х²х=±1
-11
+ - +
х∈[1;1]
решением исходного неравенства будет пересечение ответов для (1) и (2), т.е. х∈[-1;-√2/2]∪[√2/2;1]