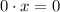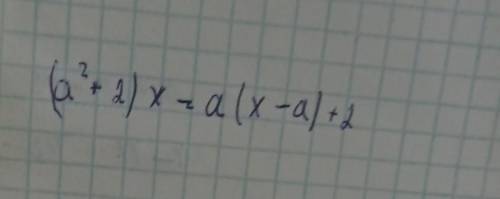
a² = 12 b² = 3
c² = a² - b² = 12 - 3 = 9 ⇒ c = 3
Фокусы имеют координаты :
F₁ (0; - c) , F₂ (0 ; c) , где c = 3
Значит F₁(0 ; - 3) , F₂(0 ; 3)
Расстояние между фокусами равно 2с, а значит равно : 2 * 3 = 6
6.2)
a² = 10 b² = 26
Аналогично
c² = 26 - 10 = 16 ⇒ c = 4
Координаты фокусов :
F₁(0 ; - 4) , F₂(0 , 4)
Расстояние между фокусами равно 2с, то есть 8.
7.1)
a² = 25 ⇒ a = 5 b² = 9 ⇒ b = 3
c² = a² - b² = 25 - 9 = 16 ⇒ c = 4
В данном случае a > b поэтому эксцентриситетом будет отношение :
e = c/a = 4/5
7.2)
a² = 7 ⇒ a = √7 b² = 16 ⇒ b = 4
В этом случае b > a , поэтому :
c² = b² - a² = 16 - 7 = 9 ⇒ c = 3
e = c/b = 3/4
х=1 у= -2
Пошаговое объяснение:
Из второго уравнения получаем: (3х+у)= -2/ху
Подставляем в первое:
-2/ху (9х²+у²)=13
-18х/у -2у/х=13
-18х-2у²/х=13у
-18х²-2у²=13ху
18х²+13ху+2у²=0
Чтобы было проще, умножим обе части на 2!
(Приводим к формуле сокращенного умножения (х+у)²)
36х²+26ху+4у²=0
6²х²+2*6*2ху+2²у²= -2ху
(6х+2у)²= -2ху
2(3х+у)²= -ху
ху=-2(3х+у)²
Подставляем это во второе уранение:
-2(3х+у)² * (3х+у)=-2
(3х+у)³=1
3х+у=1
у=1-3х
Меняем у на вычисленное во втором уравнении:
х(1-3х) (3х+1-3х)=-2
х-3х=-2
-2х=-2
х=1
Вычисляем у подставив х=1 в выражение у=1-3х:
у=1-3
у= -2
Объяснение:
Такого значения параметра а не существует!
Объяснение:
Линейное уравнение будет иметь бесконечное множество корней если оно в общем виде записывается как: