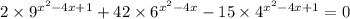
Объяснение:
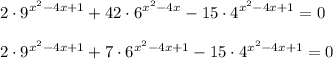
разделим обе части уравнения на 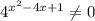
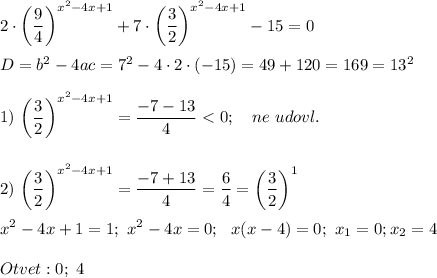
70 км/ч
Объяснение:
Туристы ехали на двухэтажном автобусе на 20 км/ч медленнее, чем туристы на микроавтобусе, и проехали расстояние 630 км, потратив на 2 часа больше туристов, которые ехали быстрее.
Найти, с какой скоростью ехали туристы на двухэтажном автобусе?
Обозначим x км/ч скорость медленных туристов на двухэтажном автобусе, тогда x+20 км/ч - скорость быстрых туристов на микроавтобусе.
Медленные приехали в Белгород за время t1 = 630/x, а быстрые за время t2 = 630/(x+20). И это время на 2 часа меньше:
t1 - t2 = 2
630/x - 630/(x+20) = 2
Умножаем всё уравнение на x(x+20):
630(x+20) - 630x = 2x(x+20)
630x + 630*20 - 630x = 2x^2 + 40x
630*20 = 2x^2 + 40x
Делим всё уравнение на 2 и переносим число вправо:
0 = x^2 + 20x - 6300
D/4 = 10^2 - 1*(-6300) = 100 + 6300 = 6400 = 80^2
x1 = (-10 - 80)/1 = -90 < 0 - не подходит.
x2 = (-10 + 80)/1 = 70 км/ч - скорость туристов на двухэтажном автобусе.
x + 20 = 70 + 20 = 90 км/ч - скорость туристов на микроавтобусе.
В решении.
Объяснение:
Дополните:
а) 6 - 2√5 = (√5 - ?)²;
Квадрат разности; формула: (а - в)² = а² - 2ав + в²;
а = √5 по условию;
Найти в:
2ав = 2√5 = 2 * √5 * в;
в = 2√5 : 2√5
в = 1;
6 - 2√5 = (√5 - 1)²;
Проверка:
(√5 - 1)² = (√5)² - 2*√5 + 1² = 5 - 2√5 + 1 = 6 - 2√5, верно;
б) 7 + 4√3 = (2 + ?)²;
Квадрат суммы; формула: (а + в)² = а² + 2ав + в²;
а = 2 по условию;
Найти в:
2ав = 4√3 = 2 * 2 * в;
в = 4√3 : 4
в = √3;
7 + 4√3 = (2 + √3)²;
Проверка:
(2 + √3)² = 4 + 4√3 + 3 = 7 + 4√3, верно;
в) 22 - 12√2 = (? - 3√2)²;
Квадрат разности; формула: (а - в)² = а² - 2ав + в²;
в = 3√2 по условию;
Найти а:
2ав = 12√2 = 2 * а * 3√2;
а = 12√2 : 6√2
а = 2;
22 - 12√2 = (2 - 3√2)²;
Проверка:
(2 - 3√2)² = 4 - 2*2*3√2 + (3√2)² = 4 - 12√2 + 18 = 22 - 12√2, верно;
г) 33 + 12√6 = (? + 3)²;
Квадрат суммы; формула: (а + в)² = а² + 2ав + в²;
в = 3 по условию;
Найти а:
2ав = 12√6 = 2 * а * 3
а = 12√6 : 6
а = 2√6;
33 + 12√6 = (2√6 + 3)²;
Проверка:
(2√6 + 3)² = (2√6)² + 2*2√6*3 + 9 = 24 + 12√6 + 9 = 33 + 12√6, верно;
д) 30 - 12√6 = (2√3 - ?)²;
Квадрат разности; формула: (а - в)² = а² - 2ав + в²;
а = 2√3 по условию;
Найти в:
2ав = 12√6 = 2 * 2√3 * в;
в = 12√6 : 4√3
в = 3√2;
30 - 12√6 = (2√3 - 3√2)²;
Проверка:
(2√3 - 3√2)² =
= (2√3)² - 2*2√3*3√2 + (3√2)² =
= 4*3 - 12√6 + 9*2 = 12 - 12√6 + 18 = 30 - 12√6, верно;
е) 50 = (√8 + ?)²;
Предыдущий приём нельзя применить, нет значения 2ав, поэтому:
(√8 + х)² = 50
(√8)² + 2*√8*х + х² = 50
8 + 2√8х + х² - 50 = 0
х² + 2√8х - 42 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = (2√8)² + 168 = 32 + 168 = 200 √D=√(25*8) = 5√8
х₁=(-b-√D)/2a
х₁=(-2√8-5√8)/2 = (-7√8)/2 = -3,5√8, отбросить, как отрицательный;
х₂=(-b+√D)/2a
х₂=(-2√8+5√8)/2
х₂=(3√8)/2
х₂=1,5√8;
в = 1,5√8;
50 = (√8 + 1,5√8)²;
Проверка:
(√8 + 1,5√8)² =
= (√8)² + 2*√8*1,5√8 + (1,5√8)² =
= 8 + 3*8 + 2,25*8 =
= 8 + 24 + 18 = 50, верно.
Воспользовавшись свойствами степеней, запишем:
Разделим уравнение почленно на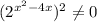 :
:
Замена: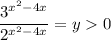
Получим уравнение:
Так как сумма коэффициентов уравнения равна 0, то первый корень равен 1, а второй равен отношению свободного члена к ставшему коэффициенту:
Обратная замена. Первое уравнение:
Второе уравнение:
На этом шаге понятно, что последнее уравнение не имеет корней, так как показательная функций не принимает отрицательных значений.
Таким образом, уравнение имеет два корня.
ответ: 0 и 4