В решении.
Объяснение:
Сократить дробь:
а) (-16с⁵)/12с³=
сократить (разделить) 16 и 12 на 4, с⁵ и с³ на с³:
=(-4с²)/3=
= -4с²/3;
б) (4a-4b)/(3a-3b)=
=4(a-b)/3(a-b)=
сократить (разделить) (a-b) и (a-b) на (a-b):
=4/3;
в) (а²-5а)/(25-а²)=
=(а²-5а)/ -(а²-25)=
=а(а-5)/ -[(а-5)(а+5)]=
сократить (разделить) (а-5) и (а-5) на (а-5):
= -а/(а+5);
г) a⁵b⁷/a⁷b⁵=
при делении показатели степеней вычитаются (при одинаковых основаниях):
сократить (разделить) а⁵ и а⁷ на а⁵, b⁵ и b⁷ на b⁵:
=1*b²/a²*1=
=b²/a²;
д) (3х³+3ху²)/(6ух²+6у³)=
=3х(х²+у²)/6у(х²+у²)=
сократить (разделить) 3 и 6 на 3, (х²+у²) и (х²+у²) на (х²+у²):
=х/2у;
е) (b²-4)/(8-b³)=
в числителе разность квадратов, развернуть, в знаменателе разность кубов, развернуть:
=[(b-2)(b+2)] / (2³-b³)=
=[(b-2)(b+2)] / -(b³-2³)=
=[(b-2)(b+2)] / -[(b-2)(b²+2b+4)]=
сократить (разделить) (b-2) и (b-2) на (b-2):
= -(b+2)/(b²+2b+4).
Пусть (1900+10х+у) - год рождения
где
х- цифра десятков
у - - цифра единиц
1+9+х+у = (10+х+у) - сумма цифр
1993 - (1900+10х+у) = (93 - 10х-у) - возраст
По условию сумма цифр равна возрасту:
10+х+у = 93-10х-у
10+х+у-93+10х+у=0
11х+2у-83=0
11х=83-2у
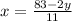
ОДЗ: 0≤x≤9;
0≤y≤9
Чтобы число х было целым, числитель (8х-2у) должен быть кратным 11.
1) при у=0 => 83-2·0=83 не делится на 11
2) при у=1 => 83-2·1=81 не делится на 11
3) при у=2 => 83-2·2=79 не делится на 11
4) при у=3 => 83-2·3=77 делится на 11, тогда х=77/11 =7
Получаем год рождения:
1900+10·7+3 = 1973
ответ: 1973
Вот
Объяснение: