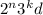, где 
, 
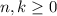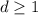и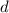 
не делится ни на 2 ни на 3. Заметим, что любое натуральное число можно представить в таком виде. Тогда по условию 
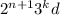должно быть квадратом, а 
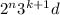должно быть кубом, т.е. 
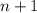и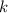 
делятся на 2, а 
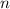и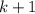 
делятся на 3, и, кроме того, 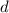является одновременно и квадратом и кубом, т.е. является 6-ой степенью. Минимальное 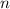, такое что оно делится на 3 и 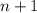делится на 2 равно 3, т.е. 
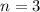. Минимальное 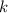, такое что оно делится на 2 и 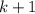делится на 3 равно 2, т.е. 
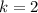. Минимальное 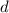, которое является 6-ой степенью равно 1. Итак, искомое число равно 
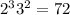. ответ: 72.
ctg(x-1) ' = -1/sin^2(x-1)
либо воспользоваться другим долгим):
ctg(x-1) = cos(x-1) / sin(x-1)
(a/b)' = (a' * b - a*b')/b^2
(cos(x-1) / sin(x-1))' = ( cos(x-1)' * sin(x-1) - cos(x-1)*sin(x-1)' ) / sin^2(x-1) = (-sin^2(x-1) - cos^2(x-1)) / sin^2(x-1) = -1/sin^2(x-1)