Відповідь: a) (-1; -4) b) x=-1 с) ОХ: (-1+√2; 0) и (-1-√2; 0) OY: (0; -2) e) в I, II, III и IV четвертях
Пояснення:
a) x=-b/2a x=-4/4=-1 y=-4
b) ось симметрии параболы - прямая, проходящая через её вершину (-1;-4) и параллельная оси Оу, поэтому абцисса ( х ) в любой точке на этой прямой одинакова и равна -1 => х = -1
c) при пересечении с осью ОХ ордината y=0 => 2x^2+4x-2=0
x1=-1+√2 x2=-1-√2
при пересечении с осью OY абсцисса х=0 y=-2
e) ветви параболы направлены вверх т.к. коэффициент а больше 0 а=2.Расположена она во всех 4-ёх четвертях

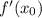 производная функции в данной точке. А
производная функции в данной точке. А  точка касания по иксу.
точка касания по иксу. мы должны найти производную общего типа этой функции.
мы должны найти производную общего типа этой функции.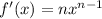 - где n это степень.
- где n это степень.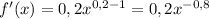


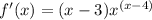
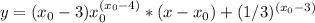
 и получаешь уравнение касательной.
и получаешь уравнение касательной.
Объяснение: