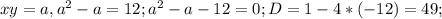
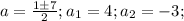, вот теперь мы можем заменить первое уравнение на более простое и решить 2 системы, объединив их решения.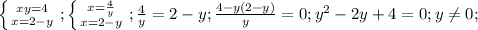 
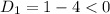, корней нет. Решаем вторую систему: 
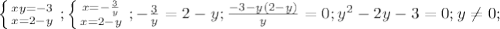Здесь b=a+c (-2=1-3), тогда 
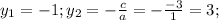, а теперь в любое уравнение подставляем каждое из получившихся и в ответе пишем 2 точки: 
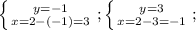, получили точки (3;-1);(-1;3). Довольно похожие значения, объясняется это всё квадратами в первом уравнении системы. ответ:(3;-1);(-1;3).
1) 4sin х=3 -> sinx=3/4 ->x=(-1)^k *arcsin 3/4 +pi*k
2)2cos3х=√3 ->cos3x=√3/2 ->3x=плюс минус pi/6 + 2pi*k -> x=плюс минус pi/18+2pi*k /3
3) 2 sin(3x-п/6)=- √3 -> 3x-pi/6 = (-1)^(k+1) * pi/3 + pi*k ->x=((-1)^(k+1) * pi)/18 +pi/18 + pi*k /3
4)arsin и arsin (-1\3)
arsin и -arsin 1\3 -> arsin > -arsin 1\3
5) cos2x= -√3 /2 -> 2x=плюс минус 5pi/6 + 2pi*k -> x= плюс минус 5pi/12 + pi*k
Подставляйте целые числа k и смотрите,какие Х подходят в промежуток
