В решении.
Объяснение:
Задание на сумму и разность кубов:
a³ + b³ = (a + b)(a² - ab + b²);
a³ - b³ = (a - b)(a² + ab + b²);
a) a³ + 8 = a³ + 2³ = (a + 2)(a² - 2a + 4);
б) 27 + m³ = 3³ + m³ = (3 + m)(9 - 3m + m²);
в) 1 - p³ = 1³ - p³ = (1 - p)(1 + p + p²);
г) c³ - 64x³ = c³ - (4x)³ = (c - 4x)(c² + 4cx + 16x²);
ґ) n⁶ - 1 = (n²)³ - 1³ = (n² - 1)(n⁴ + n² + 1) = (n - 1)(n + 1)(n⁴ + n² + 1);
д) 27a³ + b³ = (3a)³ + b³ = (3a + b)(9a² - 3ab + b²).
x₁ = 2 + 
, y₁ = 2 - 3;
x₂ = 2 -, y₂ = - 3 - 2:
Объяснение:
{ху - х = 4
{2х - у = 7
Выразим y и подставим во второе уравнение
{xy - x = 4
{-y = 7 - 2x
Уберём минус перед y, помножив выражение на (-1)
{xy - x = 4
{y = 2x - 7
Подставляем полученное выражение вместо y
x * (2x - 7) - x = 4
2x² - 7x - x =4
2x² - 8x - 4 = 0
Получаем квадратное уравнение. Сокращаем коэффиценты, деля обе стороны на 2
x² - 4x - 2 = 0
У нас a = 0. По теореме Виета: x₁ + x₂ = −b; x₁ * x₂ = c;
Но для начала проверим дискриминант
D = b² - 4ac
D = 16 - 4 * 1 * (-2)
D = 16 + 8 = 24
Нет такого натурального числа, которое было бы квадратным корнем из 24, поэтому мы не сможем решить теоремой Виета, и продолжаем решать дискриминантом
x₁,₂ = 
x₁ = 
= 
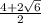= 2 +
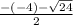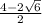x₂ = 
= 
= 2 -
Находим y, подставляя x
2 * (2 + ) - y₁ = 7
4 + 2 - y₁ = 7
- y₁ = 3 - 2
Убираем минус
y₁ = 2 - 3
Ищем y₂
2 * (2 - ) - y₂ = 7
4 - 2 - y₂ = 7
- y₂ = 3 + 2
Снова убираем минус
y₂ = - 3 - 2
ответ: x₁ = 2 + , y₁ = 2 - 3; x₂ = 2 -, y₂ = - 3 - 2;
Объяснение:
см рис
В 2) и 3) все прямые пунктиром, потому что неравенство строгое
Построение графиков(чтобы построить прямую, нужны хотя бы2 точки):
1.1 y = 5x - 4 1.2 у = -0.5х
х1 = 0 х2 = 1 х1 = 0 х2 = 2
у1 = -4 у2 = 1 у1 = 0 у2 = -1
2.1 y = 2x - 3 2.2 у = -2х + 6
х1 = 0 х2 = 2 х1 = 0 х2 = 2
у1 = -3 у2 = 1 у1 = 6 у2 = 2
3.1 y = 0.6x + 2 3.2 у = -х + 9
х1 = 0 х2 = 5 х1 = 3 х2 = 6
у1 = 2 у2 = 5 у1 = 6 у2 = 3
4.1 y = - 4/3 x - 4 4.2 у = 1/3 х + 2
х1 = 0 х2 = -3 х1 = 0 х2 = -3
у1 = -4 у2 = 0 у1 = 2 у2 = 1
а) а³+8
а³+2³
(а+2)(а²-а×2+2²)
(а+2)(а²-2а+4)
б) 27+m²
3³+m³
(3+m)(3²-3m+m²)
(3+m)(9-3m+m²)
в) 1-p³
1³-p³
(1-p)(1²+1p+p²)
(1-p)(1+p+p²)
г) с³-64х³
с³-4³х³
с³-(4х)³
(с-4х)(с²+4сх+16х²)
д) n⁶-1
(n³-1)(n³+1)
(n-1)(n²+n+2)(n+1)(n²-n+1)
е) 27а³-b³
3³a³-b³
(3a)³-b³
(3a-b)(9a²+3ab+b²)