Объяснение:
3x^2 - 11x-14=0
3x^2 +3x - 14x - 14 = 0
3x(x + 1) - 14(x + 1) = 0
(x + 1)(3x - 14) = 0
x + 1 = 0; x₁ = -1
3x - 14 = 0; 3x = 14; x = 14/3; x₂ = 4 2/3
ответ: 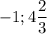
D=b² - 4ac=11²+4*3*14=121+168=289=17²
x₁=(11+17)/6=28/6=14/3
x₂=(11-17)/6=-1
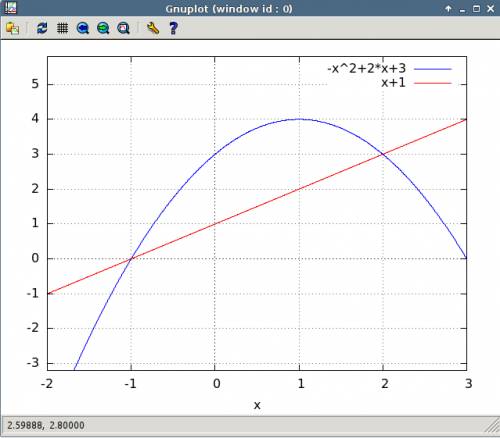
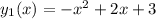 (1)
(1)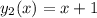 (2)
(2)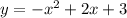 (1)
(1)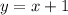 (2)
(2)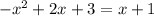
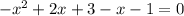
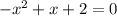 (3)
(3)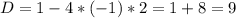
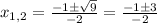
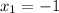
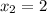
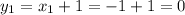
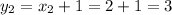
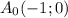

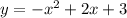 в параболу
в параболу  .
.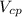 будет равен:
будет равен: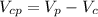 (4)
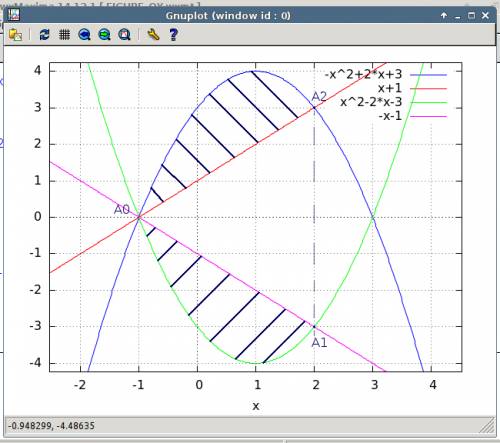
(4)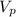 объем фигуры ограниченной, параболами и плоскостью перпендикулярной плоскости рисунка и проходящей через прямую
объем фигуры ограниченной, параболами и плоскостью перпендикулярной плоскости рисунка и проходящей через прямую 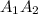 .
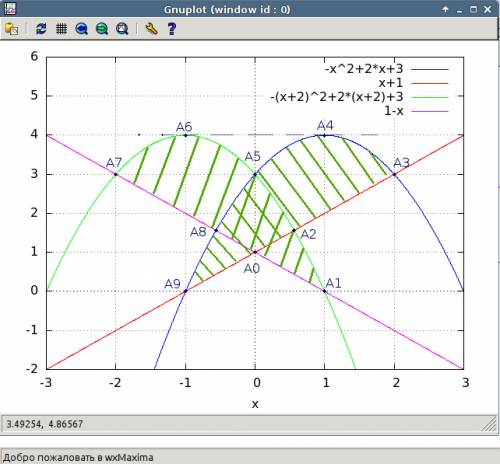
.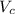 ? , объем конуса ограниченного прямыми и той же плоскостью проходящей через
? , объем конуса ограниченного прямыми и той же плоскостью проходящей через 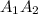
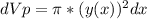
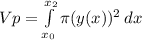 (5)
(5)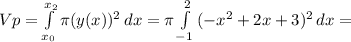
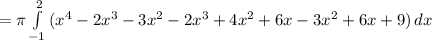
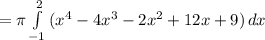 (6)
(6)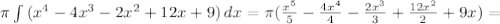
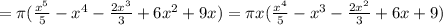 (7)
(7)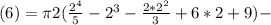
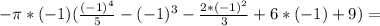
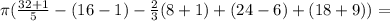
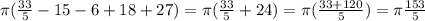 (8)
(8)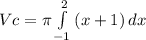 (9)
(9)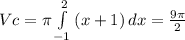 (10)
(10)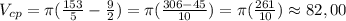
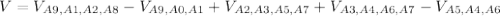
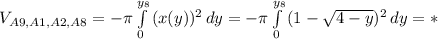
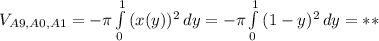

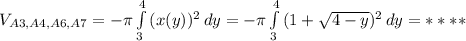

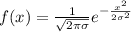 (1)
(1) 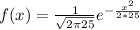 (2)
(2)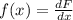 (3)
(3)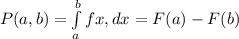 (4)
(4)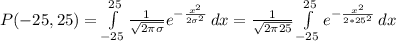 (5)
(5)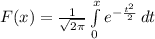 (6)
(6)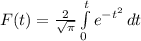 (7)
(7)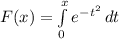 (8).
(8).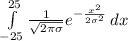
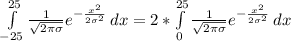 (9)
(9)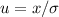 тогда
тогда 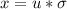
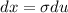
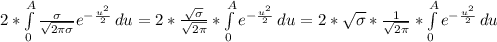 (10)
(10)
3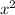 +3x-14x-14=0
+3x-14x-14=0
3x(x+1)-14x-14=0
(x+1)(3x-14)=0
x+1=0 3x-14=0
x=-1 x=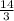
Объяснение: