с решение. 1.Представьте в виде многочлена выражение:
1)(x+9)² 3)(m-7)(m+7)
2)(3a-8b)² 4)(6a+10b) (10b-6a)
2.Расложите на множители:
1)c²-1 3)25y²-4
2)x²-4x+4 4)36a²-60ab+25b²
3.Упростите выражение: (x+3) (x-3)-(x-4)².
4.Решите уравнение: (5x-1)(x+2)+3(x-4)(x+4)=2(2x+3)²-8.
5.Представьте в виде произведения выражение:(3a-1)²-(a+2)².
6.Упростите выражение:(a-6)(a+6)(36+a²)-(a²-18)² и найдите его значение при a=-⅙
7.Докажите,что выражение x²-6x+13 принимает положительные значения при всех значениях x.
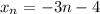
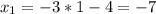

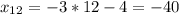

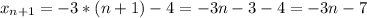
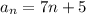
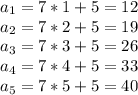


3n - 2, где n ∈ N (множеству натуральных чисел)
Для проверки подставляем 1, 2, 3 и т.д. и получаем 1, 4, 7 ...
ответ: 3n - 2
2.
Просто подставляем в формулы соответствующий индекс:
а)
б)
в)
г)
д)
3.
а) Просто берём и подставляем первые 5 индексов в формулу:
б) Просто вместо а энного подставляем 33 и решаем получившееся уравнение. Если индекс n будет целым, то число будет принадлежать данной последовательности.
Индекс n число целое, значит, 33 является членом данной последовательности. Что мы и видели, когда делали пункт 3а).
в) Делаем как в предыдущем пункте. Если число 95 не является членом последовательности, то индекс n будет дробный. Тогда округляем по правилам округления, что даст ближайший член.