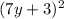
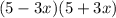
1. (7у+3)²=(7у)²+2*7у*3+3²=49у²+42у+9
2. (5-3х)(5+3х)=5²-(3х)²=25-9х²
Применяли формулы сокращённого умножения: квадрат суммы (a+b)²=a²+2ab+b² и разность квадратов (a-b)(a+b)=a²-b².
2/cos²(2x)
Объяснение:
1/3 вынесем как константу
а тангенс в кубе от двух икс это сложная функция, производная сложной функции находится как производная внешней функции умножить на производную внутренней, а у нас 2 внешних, т.е. сначала степенная( в кубе), затем от тригонометрической функции(тангенс), затем от аргумента(2х).
Начнем с внешней функции, производная внешней функции (p³)'=3p²
1/3(3*tg²(2x), теперь производная от тангенса она равна 1/cos²(2x)
1/3 и 3 сократились, остается
1/cos²(2x) умножить на производную 2х равную 2
Окончательный ответ
2/cos²(2x)
-3а>-3b ⇒ делим на (-3) и знак меняем на противоположный a < b
1) a< b
2) 2/7a< 2/7b умножили верное неравенство a < b на 2/7 - положительное число, знак неравенства не изменился
3) b-4 > a-4
верное неравенство b > a от обеих частей отняли поровну 4, знак неравенства не изменился
4) -5/9b < -5/9a
умножили верное неравенство b < a на(-5 /9 - отрицательное число, знак неравенства изменился
5)3a+2 < 3b+2
Умножили верное неравенство
a < b на 3 - положительное число, знак неравенства не изменился
и потом прибавили поровну число 2 и слева и справа
6) -5a+10> -5b+10
умножили верное неравенство a < b на (-5) - отрицательное число, знак неравенства изменился
Потом прибавление к обеим частям неравенства 10 не меняет знак.
Смотрите фото ниже.
Объяснение: