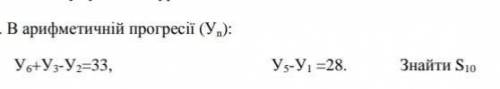
5,5, √30, 3√3
Объяснение:
1. Судя по всему что больше?
а)Взведем в квадрат 32.49>31 значит 5,7 >√31
б) тут 4,2 >0, -√17 <0 значит 4.2>-√17
но -√17 может быть и положительным, тогда так же возведем в квадрат 17,64 > 17 тот же рез-т
2: два слагаемых. одно рациональное, второе иррациональное - т. к. корень из 3 и из 7 десятичная непериодическая бесконечная дробь (не может быть представлено в виде обыкновенной дроби)
Сумма рационального и иррационального - иррациональное.
Доказывается так: сумма (разность) двух рациональных - рациональное, если в данном случае сумма (разность) будет рациональным, то оба числа в условии рациональные, а это не так, см. выше.
3. смотрим ближайшие целые квадраты: 16 и 25, т. е. между 4 и 5
4. Возведем все в квадрат и избавимся от иррациональности: 30, 27 30,25
Значит 5,5, √30, 3√3
А - сумма выпавших пунктов равна 6.
Объяснение:
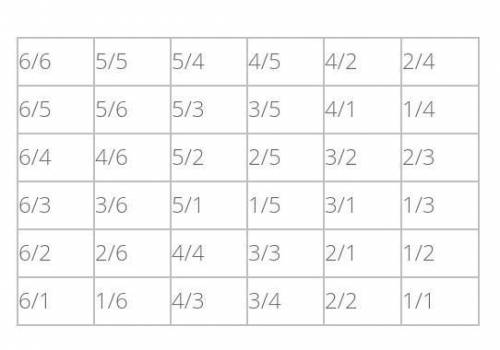
Возможные исходы, бросая два кубика, можно оформить в таблице. Первая цифра в таблице указывает, сколько пунктов выпало на первом кубике, вторая — сколько пунктов на втором кубике. Всего 36 результатов. (см. на фото)
P(события) = все исходы;
P(сумма пунктов равна 4) = 3/36 (благоприятные исходы: 3/1 и 1/3; 2/2 - вместе 3 исходов);
P(сумма пунктов равна 2) =1/36 (1/1 — только 1 благоприятный исход);
P(сумма пунктов больше 9) = 6/36 (исход благоприятный, если выпадет 10, 11 или 12 пунктов, значит, вместе 3 + 2 + 1 = 6 исходов).
У5-У1=4d, d=28:4=7
Y6+Y3-Y2=Y6+Y1=33
Y6=Y1+5d, Y1+5d+Y1=33
2Y1=33-5•7, Y1=-2/2= -1
S10= (2A1+9d)•10/2=(2•(-1)+9•7)•5=(-2+63)•5=61•5=315