y наиб = у max = 54
Объяснение:
Дана функция y= (27 - x) · √x
Производная этой функции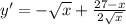 
Упростим это выражение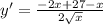 
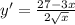
х ≠ 0 , но этот разрыв производной нас не интересует, поскольку мы ищем наибольшее значение в интервале [1; 16]
y' = 0
(27 - 3x) = 0
Точка экстремума одна x = 9.
При х < 9 y' > 0; при х > 9 y' < 0. Следовательно, точка х = 9 - точка максимума. И на концах интервала при непрерывной производной в заданном интервале значения функции будут меньше её значения в точке локального максимума.
у наиб = у max = y(9) = (27 - 9) · √ 9 = 54
1) Знак неравенства меняется если основное число меньше 1;
2) Если знак неравенства, то точка будет неполная;
3) Если знак неравенства больше равно, меньше равно, то точка будет полная.
4) Полная точка ( зарисованная внутри );
5) Неполная точка ( не зарисованная внутри );
6) Если знак неравенства, то скобка "(" ;
7) Если знак неравенства больше равно, меньше равно, то скобка
"[" ;
8) В какую сторону показывает носик неравенства, в ту сторону рисуем допустимые значения;
9) Не забываем что числа можно подавать как меньшее число в степени;
Теперь когда всё вспомнили можно решать:
1) 
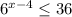
Подаём число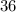 
как 
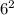
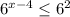
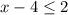
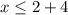
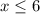
Не забываем что можно сократить основы если они одинаковые.
Теперь рисуем прямую и на ней отмечаем точку которую получили.
Фото прямых прикрепил.
Точка полная так как имеем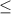 
.
Допустимые значения направленные в левую сторону так как "носик" знака неравенства направлен именно туда.
x ∈ ( -∞, 6 ]
2) 
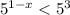
Подаём число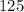 
как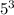 
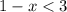
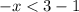
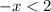
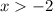
Сменили знак неравенства, так как перенесли - в другую часть неравенства.
Теперь рисуем прямую и на ней отмечаем точку которую получили.
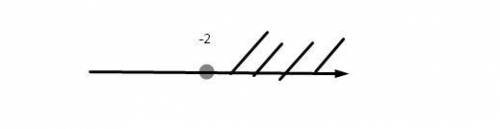
Точка неполная, так как имеем > .
x ∈ ( -2, +∞ )
3) 
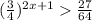
Подаём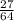 
как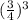 
.
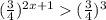
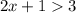
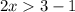
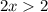
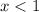
Сменили знак неравенства, так как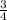 
меньше 1.
Теперь рисуем прямую и на ней отмечаем точку которую получили.
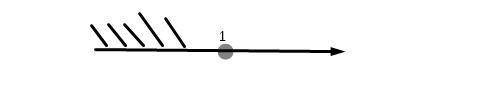
Точка неполная, так как имеем 
.
x ∈ ( -∞, 1 )
1+1=2