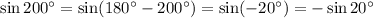Дано неравенство:
x2−x>1
Чтобы решить это нер-во - надо сначала решить соотвествующее ур-ние:
x2−x=1
Решаем:
Перенесём правую часть уравнения в
левую часть уравнения со знаком минус.
Уравнение превратится из
x2−x=1
в
(x2−x)−1=0
Это уравнение вида
a*x^2 + b*x + c = 0
Квадратное уравнение можно решить
с дискриминанта.
Корни квадратного уравнения:
x1=D−−√−b2a
x2=−D−−√−b2a
где D = b^2 - 4*a*c - это дискриминант.
Т.к.
a=1
b=−1
c=−1
, то
D = b^2 - 4 * a * c =
(-1)^2 - 4 * (1) * (-1) = 5
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
x1=12+5–√2
x2=12−5–√2
x1=12+5–√2
x2=12−5–√2
x1=12+5–√2
x2=12−5–√2
Данные корни
x2=12−5–√2
x1=12+5–√2
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
x0<x2
Возьмём например точку
x0=x2−110
=
(12−5–√2)+−110
=
25−5–√2
подставляем в выражение
x2−x>1
(25−5–√2)2−(25−5–√2)>1
2
/ ___\ ___
2 |2 \/ 5 | \/ 5 > 1
- - + |- - | +
5 \5 2 / 2
значит одно из решений нашего неравенства будет при:
x<12−5–√2
\ /
οο
x2 x1
Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
x<12−5–√2
x>12+5–√2
Решение неравенства на графике
3,5 рублей
Объяснение:
Пусть 1 кг печенья стоит х руб., тогда 1 кг конфет стоит (х + 1,3) руб.
Известно, что купили 1,2 кг конфет и это стоило 1,2(х + 1,3) руб.
Также известно, что купили 0,8 кг печенья и это стоило 0,8х
За всю покупку заплатили 1,2(х +1,3) + 0,8х, что по условию = 5, 96 руб.
Составим уравнение:
1,2(х + 1,3) + 0,8х = 5,96
1,2х + 1,56 + 0,8х = 5,96
1,2х + 0,8х = 5,96 - 1,56
2х = 4,4
х = 4,4 : 2
х = 2,2
Значит 1 кг печенья стоит 2,2 руб., тогда 1 кг конфет стоит 2,2 + 1,3 = 3,5 руб.
ответ: 3,5 рублей.
<3
Примечание:
По свойствам функций синуса и косинуса их период равен 360°:
Формулы приведения:
По определению функция косинус - четная, то есть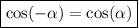
По определению функция синус - нечетная, то есть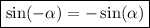
Объяснение:
а)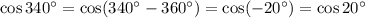
б)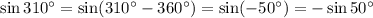
в)