Дано: ∆АВС
EF║AB; PS║BC; KM║AC;
r₁; r₂; r₃ - радиусы вписанных окружностей в ∆KPO; ∆OFM; ∆EOS.
Найти R - радиус окружности, вписанной в ∆АВС
Решение.
1)
Пусть
а - основание ∆KPO;
b - основание ∆EOS.
c - основание ∆OFM.
Но
а = КО = АЕ, как противоположные стороны параллелограмма АКОЕ.
с = ОМ = SC, как противоположные стороны параллелограмма SOMC.
Получаем
(a+b+c) - основание АС у ∆АВС.
2)
Все три внутренних треугольника подобны между собой и подобны данному ∆АВС, т.к. их соответственные стороны параллельны.
В в подобных треугольниках соответствующие стороны и все соответствующие линии пропорциональны.
Из подобия следуют три пропорциональности:
а/(a+b+c)=r₁/R;
b/(a+b+c)=r₃/R;
c/(a+b+c)=r₂/R;
Сложим эти пропорции.
а/(a+b+c) + b/(a+b+c) + c/(a+b+c)= r₁/R + r₃/R + r₂/R;
(a+b+c)/(a+b+c) = (r₁+r₂+r₃)/R;
1 = (r₁+r₂+r₃)/R;
R = (r₁+r₂+r₃).
ответ: R = r₁+r₂+r₃.

x=arcctg(3.4)
Объяснение:
5sinx+17cosx=√314.
Возведем в квадрат.25sin²x + 289cos²x + 170sinxcosx = 314.
25sin²x + 289cos²x + 170sinxcosx = 314(sin²x + cos²x)
Разделим на cos²x. (Прим: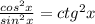 )
)25 + + 289 ctg²x + 170ctgx = 314 + 314ctg²x
314ctg²x - 289 ctg²x - 170ctgx + 314-25 = 0
25 ctg²x - 170ctgx + 289 = 0.
Заметим формулу a² - 2ab + b². Свернем по этой формуле.(5ctgx - 17)² = 0
Найдем корни данного уравнения:±(5ctgx - 17)=0
Разбиваем на два уравнения5ctgx - 17 = 0 и -5ctgx + 17 = 0
Заметим, что это одно и то же. Решим первое уравнение.5ctgx =17
ctgx = 17/5 =3.4
x=arcctg(3.4)
см ниже
Объяснение:
1) умножим уравнение на -100
8х квадрат +800х=0 разделим на 8
х квадрат +100х=0
вынесем х за скобку х(х+100)=0 произведение = 0, когда хотя бы 1 из множителей=0
х=0 или х+100=0
х=-100
ответ : х1 = 0, х2=-100
2) вынесем за скобку х
х(х-18.5)=0 как в предыдущем
х=0 или х-18.5=0
х=18.5
ответ х1=0 х2=18.5
3) перенесем 4 вправо
х= +- корень из 4
х1=2 х2= -2