Объяснение:
А)
Метод Подстановки
3х - у = 5
2х + 7у = 11
у = 3х - 5
2х + 7у = 11
1)
2х + 7у = 11
2х + 7(3х - 5) = 11
2х + 21х - 35 = 11
2х + 21х = 11 + 35
23х = 46
х = 46 : 23
х = 2
2)
у = 3х - 5
у = 3 * 2 - 5
у = 6 - 5
у = 1
ответ: (2; 1)
Б)
Метод сложения
2а + в = 5
2а - в = 11
4а = 16
2а + в = 5
1)
4а = 16
а = 16 : 4
а = 4
2)
2а + в = 5
2 * 4 + в = 5
8 + в = 5
в = 5 - 8
в = -3
ответ: (4; -3)
34/56
Объяснение:
Чтобы три случайных числа a, b, c являлись сторонами треугольника нужно выполнение условий:
a+b>c
a+c>b
b+c>a
Найдем все удачные исходы:
При первом выпадении на кубике "1":
{1,1,1}, {1,2,2}, {1,3,3}, {1,4,4}, {1,5,5}, {1,6,6} - 6 исходов.
При первом выпадении на кубике "2":
{2,2,2}, {2,2,3}, {2,3,3}, {2,3,4}, {2,4,4}, {2,4,5}, {2,5,5}, {2,5,6}, {2,6,6} - 9 исходов.
При первом выпадении на кубике "3":
{3,3,3}, {3,3,4}, {3,3,5}, {3,4,4}, {3,4,5}, {3,4,6}, {3,5,5}, {3,5,6}, {3,6,6} - 9 исходов.
При первом выпадении на кубике "4":
{4,4,4}, {4,4,5}, {4,4,6}, {4,5,5}, {4,5,6}, {4,6,6} - 6 исходов.
При первом выпадении на кубике "5":
{5,5,5}, {5,5,6}, {5,6,6} - 3 исхода.
При первом выпадении на кубике "6":
{6,6,6} - 1 исход.
Всего успешных исходов N1 = 6+9+9+6+3+1 = 34
Общее число исходов равно числу сочетаний с повторениями:
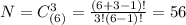
Искомая вероятность:
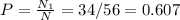


Объяснение:
а)
{3х - у = 5
{2х + 7у = 11
Выразим х через у
у = 3х - 5
Подставим во второе уравнение
2х + 7*(3х - 5) = 11
2х + 21х - 35 = 11
23х = 11 + 35
23х = 46
х = 46 : 23
х = 2
Подставим в первое уравнение х = 2
3 * 2 - у = 5
6 - у = 5
-у = 5 - 6
- у = - 1
у = 1
ответ: ( 2; 1)
б)
{2а + в = 5
{2а - в = 11
Сложим оба уравнения
4а = 16
а = 16 : 4
а = 4
Подставим во второе уравнение а = 4
2 * 4 - в = 11
8 - в = 11
-в = 11 - 8
- в = 3
в = -3
ответ: (4; -3)