Учитывая это попробуем узнать, могут ли выполняться равенства:
Поскольку по условию функция парная, то:
Любое число минус это же число = 0. Значит равенство выполняться не может. Можно это доказать. Пусть , тогда:
- не верно. Следовательно, уравнение не имеет корней и не может быть равно единице.
Поскольку по условию функция парная, то:
При умножении двух равных чисел не может получиться отрицательное число. Потому что при умножении положительных чисел получается положительное число, и при умножении отрицательных чисел также получается положительное число. То есть:
Значит равенство выполняться не может (поскольку -2 -- отрицательное число). Это можно доказать. Пусть , тогда корня квадратного из отрицательного числа не существует. Следовательно уравнение не имеет решений и не может быть равно -2.
Поскольку по условию функция парная, то:
При делении равных чисел результат всегда равен 1. Значит равенство выполняться не может. Доказательство:
Пусть , тогда . Домножим обе части уравнения на x, тогда , что не удовлетворяет ОДЗ. Значит уравнение не имеет корней и не может быть равно 0.
Путь из п. А в п. В : S₁= 27 км расстояние V₁ = х км/ч скорость t₁ = (27/x ) ч. время в пути Путь из п.В в п.А : S₂ = 27 - 7 = 20 км V₂ = (x - 2) км/ч t₂ = 20/(x-2) ч. Разница во времени : t₁ - t₂ = 12 мин. = 12/60 ч. = 0,2 ч. Уравнение: 27/х - 20/(х-2) =0,2 |* x(x-2) x≠0 ; x-2≠0 ⇒x≠2 27(х-2) - 20х = 0,2х(х-2) 27х - 54 -20х = 0,2х² - 0,4х 7х -54 = 0,2х² -0,4х 0,2х²-0,4х -7х +54 =0 0,2х² - 7,4х +54 =0 |÷0.2 x² - 37x + 270 =0 D= (-37)² -4*1*270 = 1369-1080=289=17² x₁= (37 - 17) /(2*1) = 20/2 = 10 (км/ч) x₂ = (37+17)/2 = 54/2 = 27 (км/ч) Поскольку скорость велосипеда , в зависимости от местности , в среднем составляет от 10-30 км/ч (француз Ф.Жисси , например, на своем реактивном велосипеде развил скорость более 300 км/ч) , то удовлетворяют условию оба варианта.
ответ : 10 км/ч или 27 км/ч скорость велосипедиста из пункта А в пункт В.
Функция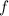 называется парной, если:
называется парной, если:
Учитывая это попробуем узнать, могут ли выполняться равенства:
Поскольку по условию функция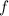 парная, то:
парная, то:
Любое число минус это же число = 0. Значит равенство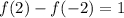 выполняться не может. Можно это доказать. Пусть
выполняться не может. Можно это доказать. Пусть 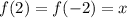 , тогда:
, тогда:
Поскольку по условию функция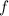 парная, то:
парная, то:
При умножении двух равных чисел не может получиться отрицательное число. Потому что при умножении положительных чисел получается положительное число, и при умножении отрицательных чисел также получается положительное число. То есть:
Значит равенство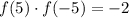 выполняться не может (поскольку -2 -- отрицательное число). Это можно доказать. Пусть
выполняться не может (поскольку -2 -- отрицательное число). Это можно доказать. Пусть 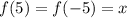 , тогда
, тогда 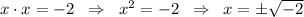 корня квадратного из отрицательного числа не существует. Следовательно уравнение не имеет решений и
корня квадратного из отрицательного числа не существует. Следовательно уравнение не имеет решений и 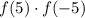 не может быть равно -2.
не может быть равно -2.
Поскольку по условию функция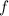 парная, то:
парная, то:
При делении равных чисел результат всегда равен 1. Значит равенство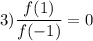 выполняться не может. Доказательство:
выполняться не может. Доказательство:
Пусть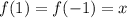 , тогда
, тогда 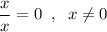 . Домножим обе части уравнения на x, тогда
. Домножим обе части уравнения на x, тогда 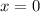 , что не удовлетворяет ОДЗ. Значит уравнение не имеет корней и
, что не удовлетворяет ОДЗ. Значит уравнение не имеет корней и 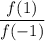 не может быть равно 0.
не может быть равно 0.