
Объяснение:
Для разложения многочлена на множители найдем его корни (напомним, что корнями многочлена называются числа, которые превращают его в  ).
).
Согласно следствию из теоремы Безу целые корни такого многочлена следует искать среди делителей свободного члена. Делителями числа  являются числа
являются числа 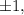




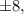

 Последовательно начиная подставлять их в указанной последовательности, убеждаемся, что одним из корней данного многочлена является число
Последовательно начиная подставлять их в указанной последовательности, убеждаемся, что одним из корней данного многочлена является число 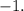 Это означает, что можно выделить линейный множитель, записав
Это означает, что можно выделить линейный множитель, записав 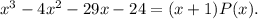
Для нахождения  выполним деление
выполним деление  на
на  в столбик (см. рисунок). Получаем в частном квадратный трехчлен
в столбик (см. рисунок). Получаем в частном квадратный трехчлен  корни которого легко найти с теоремы Виета. Сумма корней должна быть равна
корни которого легко найти с теоремы Виета. Сумма корней должна быть равна  а их произведение —
а их произведение —  Легко подобрать такую пару чисел:
Легко подобрать такую пару чисел:  и
и  Тогда
Тогда 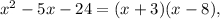 а исходный многочлен раскладывается на множители следующим :
а исходный многочлен раскладывается на множители следующим : 

Объяснение:
Александр упаковал 400 больших коробок и израсходовал два рулона скотча полностью, а от третьего осталось ровно две пятых,то есть:
2+(1-(2/5))=2+(3/5)=2³/₅ (рулона).
65 см=0,65 м 55 см=0,55 м.
Найдём количество метров в одном рулоне:
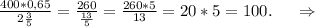
Количество метров в трёх рулонах скотча: 100*3=300. ⇒
Если на каждую коробку нужно по 0, 55 м скотча, то на 560 одинаковых коробок ему нужно:
560*0,55=308 (м) ⇒
ответ: трёх целых таких рулонов скотча ему не хватит.
Общий вид функции
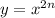
Верное свойство данной функции 3):
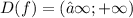
Объяснение:
Я так понимаю, имелось в виду следующее:
Дана функция
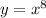
Общий вид данной функции:
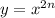
Потому что показатель степени у данной функции равен 8, т е. четный:
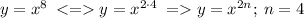
Выбери верное свойство данной функции:
1.D(f)=(−∞;0] - Неверно.
Данная функция определена как для положительных, так и для отрицательных значений аргумента
![1. \quad \: \cancel{D(f)=(−∞;0] } \\](/tpl/images/1610/0071/c3970.png)
2. Ф-ия нечётная - НЕверно
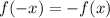
Проверим функцию на нечетность. Нечетной называется функция, если f(-x) = -f(x)
В нашем случае

3. D(f)=(−∞;+∞) - ВЕРНО!
ДАННАЯ ФУНКЦИЯ ОПРЕДЕЛЕНА ДЛЯ ЛЮБЫХ ДЕЙСТВИТЕЛЬНЫХ ЗНАЧЕНИЙ Х:
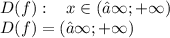
(x+1)(x-8)(x+3)
Объяснение:
x^3-4x^2-29x-24=x^3+x^2-5x^2-5x-24x-24=x^2(x+1)-5x(x+1)-24(x+1)=(x+1)(x^2-5x-24)=(x+1)(x^2-8x+3x-24)=(x+1)(x(x-8)+3(x-8))=(x+1)(x-8)(x+3)