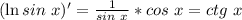решение смотри на фотографии

a = 3
Объяснение:
Имеем выражение:
a^2 - 6 * a + 11.
Необходимо найти значение аргумента a, при котором значение выражения будет минимальным.
Здесь можно приравнивать значение выражения к нулю, можно решать квадратное уравнение, можно искать значение переменной методом подбора, но единственный практичный выделить у выражения квадрат суммы или разности двух чисел:
a^2 - 6 * a + 11 = a^2 - 2 * 3 * a + 3 * 3 + 2 = (a - 3)^2 + 2.
Получили сумму квадрата числа и двойки. Наименьшее значение суммы - 2, значит, a = 3.
ОДЗ первого неравенства находим из условия
х-2>0⇒x>2
x+2>0⇒x>-2
Значит, ОДЗ х>2, или х∈(2;+∞), а второго
(x-2)(x+x)>0 найдем решения методом интервалов.
х=2, х=-2,
-22
+ - +
х∈(-∞;-2)∪(2;+∞)
я ВЫДЕЛИЛ Вам жирным шрифтом ОДЗ, видите разницу? Так вот применение свойства
㏒ₐx+㏒ₐy=㏒ₐ(xy) расширяет область определения на интервал
(-∞;-2)
поэтому, решая первое неравенство системы, (x-3)*(x+3)>0
-33
+ - +
Вы получите лишний промежуток, а именно (-∞;-3), входящий в интервал (-∞;-2); его надо исключить из ответа.
1) (sin x+cos x)²= 1 + sin2x ⇒ (1 + sin2x)' = 2cos2x ⇒ ((sin x+cos x)²)' = 2cos2x
2)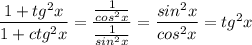
⇒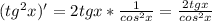 ⇒
⇒ ![\left[\begin{array}{c}\dfrac{1+tg^2x}{1+ctg^2x}\end{array}\right] ' = \dfrac{2tgx}{cos^2x}](/tpl/images/0921/6703/6cb0a.png)
3)