y' = - 2 (sin (8x)) ' (8x)'= - 2 * 8 cos 8x=-16 cos8x
f '(x0) = - 16 cos8 x0
f '( pi/6)=
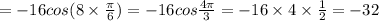
k=tga=y'(x0)
по геометрическому смыслу производной
Парабола: определение, свойства, построение
Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
y2=2px
при условии p>0.
Из уравнения (1) вытекает, что для всех точек параболы x≥0. Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.
Форма параболы известна из курса средней школы, где она встречается в качестве графика функции y=ax2. Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством 2p=a−1.
Фокусом параболы называется точка F с координатами (p/2,0) в канонической системе координат.
Директрисой параболы называется прямая с уравнением x=−p/2 в канонической системе координат
Утверждение.
Расстояние от точки M(x,y), лежащей на параболе, до фокуса равно
r=x+p2
Доказательство.
Вычислим квадрат расстояния от точки M(x,y) до фокуса по координатам этих точек: r2=(x−p/2)2+y2 и подставим сюда y2 из канонического уравнения параболы. Мы получаем
r2=(x−p2)2+2px=(x+p2)2.
Отсюда в силу x≥0 следует равенство
Парабола: определение, свойства, построение
Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
y2=2px
при условии p>0.
Из уравнения (1) вытекает, что для всех точек параболы x≥0. Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.
Форма параболы известна из курса средней школы, где она встречается в качестве графика функции y=ax2. Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством 2p=a−1.
Фокусом параболы называется точка F с координатами (p/2,0) в канонической системе координат.
Директрисой параболы называется прямая с уравнением x=−p/2 в канонической системе координат
Утверждение.
Расстояние от точки M(x,y), лежащей на параболе, до фокуса равно
r=x+p2
Доказательство.
Вычислим квадрат расстояния от точки M(x,y) до фокуса по координатам этих точек: r2=(x−p/2)2+y2 и подставим сюда y2 из канонического уравнения параболы. Мы получаем
r2=(x−p2)2+2px=(x+p2)2.
Отсюда в силу x≥0 следует равенство
всё во вложении
-16 cos 8 x0 это выражение.Теперь полставим значение
-16cos 8 -(п/6)=-16 cos (-4п/3)=-16×(-1/2)=8