натуральное число, тогда 
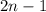будет натуральным и нечётным числом. Возведем данное число в квадрат: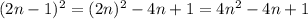
, 0 делиться на 8, следовательно условие выполняется.. Докажем что данное число делиться на 8 при 
:
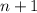делиться на 8. Следовательно, существует натуральный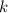 
так что: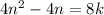
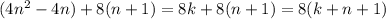следовательно, при 
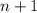данное число тоже делиться на 8. Ч.Т.Д.
100mng=100mng
100=100
тождество
б)10x²·2y²·3z³=60x²2y²3z³
60x²2y²3z³=60x²2y²3z³
60=60
тождество
в)7a·2b·3c=42abc
7a·2b·3c=42abc
42abc=42abc
42=42
тождество
г)17p²·2g²·0,5s³=17p²g²s³
17p²g²s³=17p²g²s³
17=17
тождество