Объяснение:
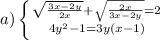сделаем замену 
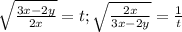тогда выйдет , 
=> 
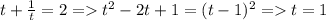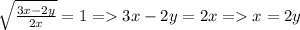подставим это во вторую систему , 
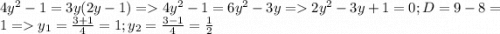из чего исходя будет два решения первое 
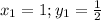второе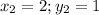 
![b)\left \{ {{\sqrt{x+y}+\sqrt[3]{x-y} =6} \atop {\sqrt[6]{(x+y)^3(x-y)^2} x=8}} \right.](/tpl/images/2004/3737/3ad52.png)
сделаем замену ![a=\sqrt{x+y} ; b=\sqrt[3]{x-y}](/tpl/images/2004/3737/bfde5.png)
=> ![\left \{ {{a+b=6} \atop {\sqrt[6]{a^6*b^6} =2}} \right. =\left \{ {{a+b=6} \atop {ab=8}} \right. =a=4 ; b=2](/tpl/images/2004/3737/23a4c.png)
или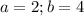 
тогда выйдет ![2)\left \{ {\sqrt{x+y}=4 } \atop { \sqrt[3]{x-y}=2}}} \right.=+\left \{ {{x+y=16} \atop {x-y=8}} \right. = x=12 ; y=4](/tpl/images/2004/3737/73934.png)
![1)\left \{ {\sqrt{x+y}=2 } \atop { \sqrt[3]{x-y}=4}}} \right.=+\left \{ {{x+y=4} \atop {x-y=64}} \right. = x=34 ; y=-30](/tpl/images/2004/3737/2f757.png)
тогда будет два решения 1) (12;4) 2) (34;-30)
227
Объяснение:
f(x)=x⁴-2x²+3
находим производную:
f'=(х⁴-2x²+3)'=4х³-2*2х+0= 4х³-4х
приравниваем производные к 0:
f' = 4x³-4x=0
находим критические точки:
4x³-4x=0
4х(х²-1)=0
4х(х-1)(х+1)=0
х=0 или х-1=0 или х+1=0
х1=0, х2=1, х3=-1
смотри прикрепленное изображение 1
необходимо найти наибольшее значение на промежутке [-4;3] (прикрепленное изображение 2)
Для нахождения наибольшего значения функции на заданном отрезке достаточно вычислить её значения на концах отрезка ( х=-4 и х=3 ) и в точке максимума (х=0).
f(x)=x⁴-2x²+3 →
Эти значения функции:
f(-4)=(-4)⁴-2*(-4)²+3=256-32+3=227
f(0)=0⁴-2*(0)²+3=0-0+3=3
f(3)=(3)⁴-2*(3)²+3=81-18+3=66 →
Наибольшее значение функции в точке х=-4 и f(x)=227
![Разве в функции на отрезке [-4; 3] наибольшее значение функции не равно 227? Просто в другом вопрос](/tpl/images/2004/3431/b8b35.jpg)
![Разве в функции на отрезке [-4; 3] наибольшее значение функции не равно 227? Просто в другом вопрос](/tpl/images/2004/3431/00b1c.jpg)
х (5х - 15) = 0
х = 0 5х - 15 = 0
5х = 15
х = 3