Объяснение:
Вообще в этом примере скобки мы можем опустить.
Получим:
2,56 * 10^-4 * 4,5 * 10^7
Для удобства десятичные дроби сгруппируем в одной части, а десятки в другой. Имеем:
2,56 * 4,5 * 10^-4 * 10^7
2,56 * 4,5 = 11,52
10^-4 * 10^7 = 10^7+(-4) = 10^3
(При умножении показатели степеней складываются. Если не знаешь свойства степеней - бегом открывай учебник по алгебре за 7 класс и учи. Это пригодится в дальнейшем!)
Получили 11,52 * 10^3 - это не стандартный вид числа. Число, стоящее перед 10 в кубе должно быть меньше 10. Следовательно, у 11,52 мы отбрасываем влево запятую, и степень числа 10 увеличивается на 1.
И мы получаем окончательный ответ:
1,152 * 10^4 - это уже стандартный вид числа.
Задача решена.
.
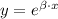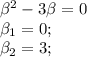
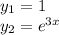
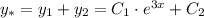
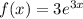
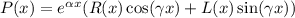, где R(x) и S(x) - полиномы, которое имеет частное решение.
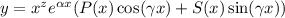, где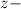 
кратность корня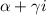 
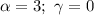
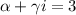является корнем характеристического уравнения кратности z=1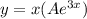
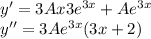
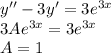
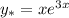
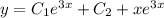
{a + aq + aq^2 = 42
{1/a + 1/(aq) + 1/(aq^2) = 21/32
{a(1 + q + q^2) = 42
{(q^2 + q + 1) / (aq^2) = 21/32
{(1 + q + q^2) = 42/a
{42/(a*aq^2) = 21/32
2/(a^2q^2) = 1/32
a^2q^2 = 64
aq = 8
(1 + q + q^2) делится на 7
Нетрудно догадаться, что:
a = 2, q = 4
1 + q + q^2 = 1 + 4 + 16 = 21
a1 = a = 2, a2 = aq = 8, a3 = aq^2 = 32