3 мин =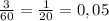 
часа
Пусть х дет. обрабатывал рабочий на старом станке за шестичасовую смену, тогда
(х+10) дет. обрабатывает рабочий на новом станке за шестичасовую смену
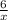час на обработку одной детали на старом станке
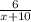час на обработку одной детали на новом станке
По условию рабочий на новом станке экономит 3 минуты при обработке одной детали.
Уравнение
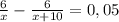
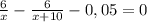
ОДЗ: x>0; x≠10
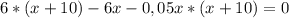
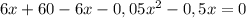
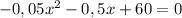
Делим обе части уравнения на (- 0,05) и получаем:
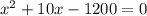
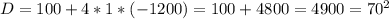
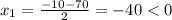
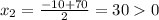
30 дет. обрабатывал рабочий на старом станке за шестичасовую смену
30+10= 40 дет. обрабатывает рабочий на новом станке за шестичасовую смену
ответ: 40
дана фунция y=x²-2x-8
проанализируем
1) Графиком будет парабола, ветви вверх
2) вершина параболы
x₀= -b/2a= -(-2)/2*1=1
y₀=1²-2*1-8= -9
Значит вершина в точке (1; -9)
3) найдем нули функции
x²-2x-8=0
D=4+32=36
x₁.₂= (2±6)/2
x₁=4; x₂=-2
Значит нули в точках (-2;0) и (4;0)
4) Теперь рассмотрим наш отрезок [-1;3].
в этот отрезок попадает вершина параболы, значит наименьшее значение у= -9
заметим, что точки -1 и 3 симметрично отличаются от нулей функции
значит значения функции в этих точках равны
найдем их
у(-1)=(-1)²-2*(-1)-8=1+2-8= -5
Наша функция от точки х= -1 до точки х= 1 убывает, а от точки х=1 до точки х= 3 возрастает
Значит наименьшее значение в вершине у= -9
наиболшее в концах отрезка у= -5
Тогда область значений на отрезке x∈[-1;3] будет y ∈ [-9;-5]
(4x^2-1-3x^2)/(x+1)^2=(x^2-1)/(x+1)^2=(x+1)(x-1)/(x+1)^2=(x-1)/(x+1)