14х^2-5х-1
10х^2-13 х + 4
14х^2-5x-1=14(x-1/2)(x+1/7)
D=25-4*14*(-1)=25+56=81
x1=(5+9):28=14/28=1/2; x2=(5-9):28=-4/28=-1/7
10х^2-13 х + 4=10(x-4/5)(x-1/2)
D=169-4*10*4=169-160=9
x1=(13+3):20=4/5; x2=(13-3):20=10/20=1/2
14х^2-5х-1 = 14(x-1/2)(x+1/7)= 7(x+1/7)=7x+1
10х^2-13 х + 4 10(x-4/5)(x-1/2) 5(x-4/5) 5x-4
В решении.
Объяснение:
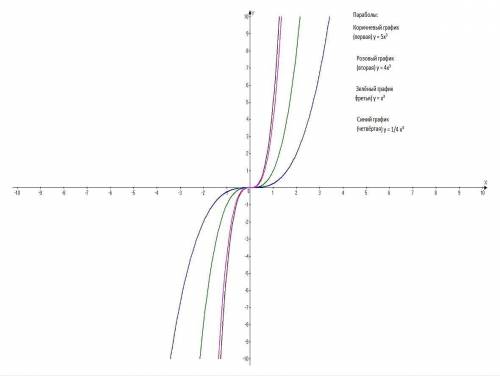
Построить в одной системе координат графики функций:
у = х³; у = 5х³; у = х³/4; у = 4х³.
Все графики - кубические параболы с вершиной в начале координат (0; 0). у = х³ - классическая парабола, остальные, в зависимости от коэффициента перед х³ "уже" или "шире" её.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
1) у = х³;
Таблица:
х -2 -1 0 1 2
у -8 -1 0 1 8
2) у = 5х³;
Таблица:
х -2 -1 0 1 2
у -40 -5 0 5 40
3) у = 1/4 х³ = х³/4;
Таблица:
х -3 -2 -1 0 1 2 3
у -6,75 -2 -0,25 0 0,25 2 6,75
4) у = 4х³;
Таблица:
х -2 -1 0 1 2
у -32 -4 0 4 32
Вероятность определяется как отношение числа благоприятных исходов к общему числу исходов. Всего исходов 12, так как есть 12 номеров.
A — «номер является чётным числом»
Подходящие номера: 2, 4, 6, 8, 10, 12 - 6 номеров
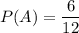
B — «номер делится на 5»
Подходящие номера: 5, 10 - 2 номера
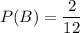
C — «номер делится на 9»
Подходящий номер: 9 - 1 номер

D — «номер меньше или равен 2»
Подходящие номера: 1, 2 - 2 номера
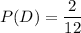
E — «номер больше, чем 2, и меньше, чем 7»
Подходящие номера: 3, 4, 5, 6 - 4 номера
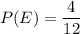
F — «номер является простым числом»
Подходящие номера: 2, 3, 5, 7, 11 - 5 номеров
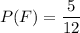
если нужно было просто сократить дробь , то смотри прикреплённый файл