Найдите сумму первых двенадцати членов арифметической прогрессии 33; 29; 25

👇

Увидеть ответ

Ответ:

igorbaburin67

16.10.2020

A1=33
d=29-33=-4
S12=(2a1+11d)/2*n=(66-44)/2*12=11*12=132

4,8(40 оценок)

Ответ:

ALEXX111111111

16.10.2020

33;29;25
разность=d=29-33=-4
S12=2a1+(n-1)d*n/2
S12=2*33+(12-1)*-4*12/2=264/2=132
ответ:S12=132

4,8(35 оценок)

Открыть все ответы

Ответ:

Ррргчг2424

16.10.2020

sin²x + 2sinx×cosx - 3cos²x + 2 = 0

sin²x + 2sinx×cosx - 3cos²x + 2×1 = 0

sin²x + 2sinx×cosx - 3cos²x + 2(sin²x + cos²x) = 0

sin²x + 2sinx×cosx - 3cos²x + 2sin²x + 2cos²x = 0

3sin²x + 2sinx×cosx - cos²x = 0 | ÷ cos²x

3tg²x + 2tan x - 1 = 0

Пусть tg x = a, тогда:

3a² + 2a - 1 = 0

D = 2² - 4×3×(-1) = 4 + 12 = 16

x₁ = -2+√16/2×3 = -2+4/6 = 2/6 = 1/3

x₂ = -2-√16/2×3 = -2-4/6 = -6/6 = -1

tg x = 1/3 или tg x = -1

x₁ = arctg(1/3) + πn x₂ = arctg(-1) + πn

x₁ = 0,321751 + πn x₂ = 3π/4 + πn

x₁ = 18,4° + πn, n∈Z x₂ = 135° + πn, n∈Z

4,4(9 оценок)

Ответ:

Danfdffefd

16.10.2020

Исходное неравенство распадается на совокупность систем:

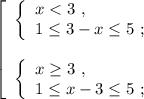
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ 1 \leq 3-x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1 \leq x-3 \leq 5 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -5 \leq x-3 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1+3 \leq x \leq 5+3 \ ; \end{array}\right \end{array}\right$

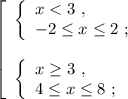
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -2 \leq x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 4 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ -2 ; 2 ] \ , \\ x \in [ 4 ; 8 ] \ ; \end{array}\right$

$x \in [ -2 ; 2 ] \cup [ 4 ; 8 ] \ ;$

а) неравенство эквивалентно:

$-2 \leq x \leq 2 \ ;$

$x \in [ -2 ; 2 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

б) неравенство эквивалентно:

$-2 \leq x-6 \leq 2 \ ;$

$6-2 \leq x \leq 2+6 \ ;$

$x \in [ 4 ; 8 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

в) неравенство эквивалентно:

$-1 \leq x \leq 1 \ ;$

$x \in [ -1 ; 1 ] \ ;$

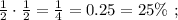
Отрезок данного решения составляет половину от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

г) неравенство распадается на совокупность систем:

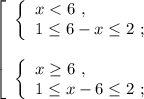
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 1 \leq 6-x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1 \leq x-6 \leq 2 \ ; \end{array}\right \end{array}\right$

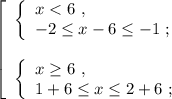
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ -2 \leq x-6 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1+6 \leq x \leq 2+6 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 4 \leq x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 7 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ 4 ; 5 ] \ , \\ x \in [ 7 ; 8 ] \ ; \end{array}\right$

$x \in [ 4 ; 5 ] \cup [ 7 ; 8 ] \ ;$

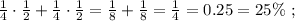
Каждый из двух отрезков данного решения составляет четверть от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{4} \cdot \frac{1}{2} + \frac{1}{4} \cdot \frac{1}{2} = \frac{1}{8} + \frac{1}{8} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

4,4(14 оценок)

Это интересно:

Стиль-и-уход-за-собой

26.11.2020

Как сделать боб каре как у Пэрис Хилтон...

Кулинария-и-гостеприимство

31.05.2023

Как приготовить банановый смузи без блендера: простые и эффективные методы...

Дом-и-сад

26.01.2022

Как выложить пол керамической или керамогранитной плиткой: советы и рекомендации...

27.05.2020