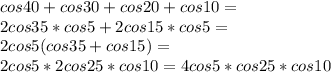
Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться, такую группу уравнений мы называем системой.
Объединяем уравнения в систему с фигурной скобки:
Графический метод
Недаром ответ записывается так же, как координаты какой-нибудь точки.
Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.
Например, построим графики уравнений из предыдущего примера.
Пример 1
Для этого сперва выразим yyy в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно xxx):
⎧
⎪⎪⎪
⎪
Для того чтобы графически решить систему уравнений с двумя переменными нужно:
1) построить графики уравнений в одной системе координат;
2) найти координаты точек пересечения этих графиков (координаты точек пересечения графиков и есть решения системы);
Разберем это задание на примере.
Решить графически систему линейных уравнений.
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Пример 2
reshenie2_598x318
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может:
а) иметь единственное решение;
б) не иметь решений;
в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Пример 3
Графическое решение системы
Пример 4
Решить графическим систему уравнений.
Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.
Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
ответ: (4; 5).
Пример 5
Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
ответ: (-2; 5).
ответ:1.Треугольники равны по первому признаку равенства треугольников-если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника,то эти треугольники равны между собой
2.Треугольники равны по третьему признаку равенства треугольников-если три стороны одного треугольника равны трём сторонам другого треугольника,то эти треугольники равны между собой
3.Треугольники равны по второму признаку равенства треугольников-если сторона и прилежащие к ней углы одного треугольника равны стороне и двум прилежащим к ней углам второго треугольника,то такие треугольники равны между собой
4.Треугольники не равны,хотя есть две одинаковые стороны и угол,но первый признак равенства треугольников гласит-если две стороны и УГОЛ МЕЖДУ НИМИ
5.Треугольники равны по первому признаку равенства треугольников
6.Треугольники не равны,хотя есть два равных угла и одна сторона,но по второму признаку равенства треугольников надо,чтобы была сторона и ПРИЛЕЖАЩИЕ к ней углы
7.Равны по третьему признаку равенства треугольников
8.Не равны,в наличии есть две стороны и угол,но надо,чтоб угол был МЕЖДУ сторонами
9.Не равны,тут только сторона и угол
10.Эти Треугольники равны между собой по второму признаку равенства треугольников
Объяснение: