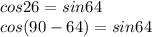то есть наше выражение в тоге равна 32
Для решения запишем формулу бинома Ньютона:
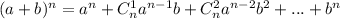
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение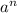 
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение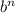 
.
Рассмотрим многочлен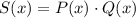 
, где:
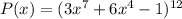
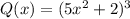
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена :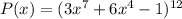
- степень определяется выражением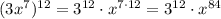 
, то есть степень равна 84
- свободный член равен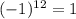 
Для многочлена :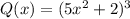
- степень определяется выражением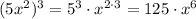 
, то есть степень равна 6
- свободный член равен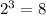 
Наконец, для многочлена 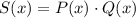получим:
- степень определяется выражением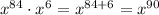 
, то есть степень равна 90
- свободный член равен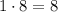 
Сумма степени и свободного члена многочлена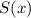 
:
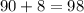
ответ: 98
Объяснение:
Решаются они все одинаково, разложением квадрата:
(x + y)^2 = x^2 + 2xy + y^2
1) (3x - 4y)^2 = (3x)^2 - 2*3x*4y + (4y)^2 = 9x^2 - 24xy + 16y^2
2) (5a + 6b)^2 = (5a)^2 + 2*5a*6b + (6b)^2 = 25a^2 + 60ab + 36b^2
3) (1/2*a + 2/3*b)^2 = a^2/4 + 2/3*ab + 4b^2/9
4) (1/4*x + 2/5*y)^2 = x^2/16 + 1/5*xy + 4/25*y^2
5) (0,1m - 0,3n)^2 = 0,01m^2 - 0,06mn + 0,09n^2
6) (0,5a + 0,2c)^2 = 0,25a^2 + 0,2ac + 0,04c^2
1) (x^2 + 2y^3)^2 = x^4 + 4x^2*y^3 + 4y^6
2) (3m^3 - m^2)^2 = 9m^6 - 6m^5 + m^4
3) (1/3*a^2*b - b^2)^2 = 1/9*a^4*b^2 - 2/3*a^2*b^3 + b^4
4) (x^3 + 1/4*xy^2)^2 = x^6 + 1/2*x^4*y^2 + 1/16*x^2*y^4
5) (-a^2*b - b^3)^2 = (a^2*b + b^3)^2 = a^4*b^2 + 2a^2*b^4 + b^6
6) (-3b^2 - c^3)^2 = (3b^2 + c^3)^2 = 9b^4 + 6b^2*c^3 + c^6
