9x^2 - 4x - 2 = 0
a = 9, b = -4, c = -2
D = b^2 - 4ac
D = (-4)^2 - 4 * 9 * (-2) = 16 + 72 = 88
ответ: D = 88 .
![lim_{x\to \infty }\frac{x+1}{x-2}=lim_{x\to \infty }\frac{\frac{x}{x}+\frac{1}{x}}{\frac{x}{x}-\frac{2}{x}}=lim\frac{1+\frac{1}{x}}{1-\frac{2}{x}}=[\frac{1+0}{1-0}]=\frac{1}{1}=1](/tpl/images/0237/6916/b2fde.png)
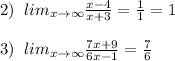
![lim_{x\to \infty }\frac{x+3}{5x^2+2x-5}=0,tak\; \; kak\\\\lim_{x\to \infty }\frac{\frac{x}{x^2}+\frac{3}{x^2}}{\frac{5x^2}{x^2}+\frac{2x}{x^2}-\frac{5}{x^2}}=lim\frac{\frac{1}{x}+\frac{3}{x^2}}{5+\frac{2}{x}-\frac{5}{x^2}}=[\frac{0+0}{5+0-0}]=\frac{0}{5}=0](/tpl/images/0237/6916/32e6e.png)
1. Здесь в условии опечатка, скорее всего в точке x₀ = -1.
Прямая y=x-2 касается графика функции y=f(x) в точке x₀ = -1, то эта точка является общей для обеих функций, тогда f(-1) = -1-2=-3
ответ: -3.
2. Производная функции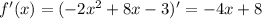 
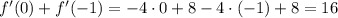
ответ: 16.
3. 
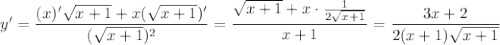
4. Производная функции: 
Используем геометрический смысл производной: f'(x₀) = tgα
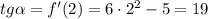
ответ: 19.
5. 
6. 
Производная функции: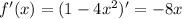 
. Производная функции в точке 1, равна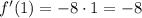 
7. Производная функции: f'(x) = 1/2√x, ее значение в точке х=1 равна 1/2. Тогда касательная: y = f'(x0)(x-x0) + f(x0) = 1/2 * (x-1) + 1 = x/2 + 1/2
y(31) = 31/2 + 1/2 = 32/2 = 16
ответ: 16.
8. 
D=b^2-4ac
9х^2-4х-2=0
D=(-4)^2-4*(9*(-2))=16+72=88
ответ:88