Сначала разделим левую и правую часть уравнения на x, получим:
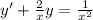
Решим сначала однородное уравнение, вида:
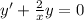
Это уравнение с разделяющимися переменными, получаем: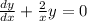
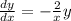
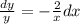
Берем интеграл от обоих частей получаем:
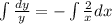
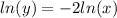
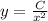
Дальше методом вариации свободной постоянной ищем частное решение неоднородного уравнения:
Представляем C как функцию от х, т.е C=C(x) и подставляем выражение 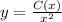 в исходное уравнение. Получаем:
в исходное уравнение. Получаем:
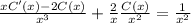
Сокращаем подобные и прочее, получаем:
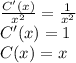
Подставляем получившееся значение C(x) в выражение 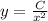 и получаем частное решение
и получаем частное решение 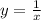
В итоге общее решение неоднородного уравнения это сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Т.е.
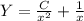
Все, уравнение решено. Теперь решаем задачу Коши:
Т.к. 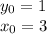
то приходим к уравнению 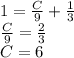
Все, нашли С, теперь пишем решение задачи Коши:
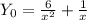
ответ: Общее решение дифференциального уравнения:
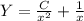
Частное решение дифференциального уравнения, удовлетворяющиего начальному условию 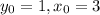 :
:
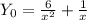
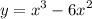
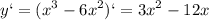
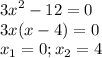
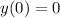 - максимальное значение
- максимальное значение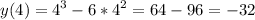 -минимальное значение
-минимальное значение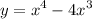
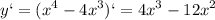
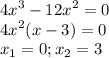
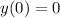 максимальное значение функции
максимальное значение функции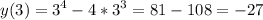 минимальное значение функции
минимальное значение функции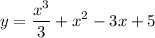
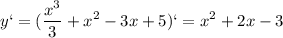
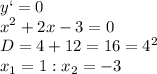
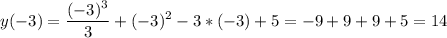
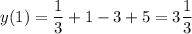 минимальное значение
минимальное значение
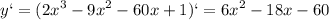
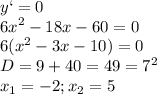
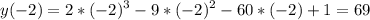
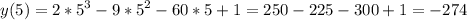
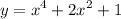
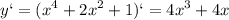
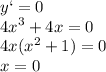
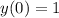
за место y 3+x.
3+x+x= 21; 2x= 21-3; 2x=18; x=9. можно x подставить в любое уравнение, и получается, что y=12.
ответ: (9,12)