Переведем все значения в градусы, чтобы было привычнее.
π=180°
/ - так обозначается черта дроби.
переведу число -0,5 в дробь, тоже для удобства = -1/2
sin(180°/4-a) если cos a = -1/2 ; 180°/2<a<180°
sin(45°-a) если cos a= -1/2;
90<a<180° по условию угол находится во второй четверти. Синус в этой четверти принимает только положительные значения.
Как найти sin a? Вспомним основное тригонометрическое тождество:
cos²a+sin²a=1, отсюда выразим наш синус:
sin²a= 1-cos²a.
Чтобы найти sin a, возведем в корень 1-cos²a
Получаем: sin a = √1-cos²a.
Подставляем известное нам выражение cos a, которое мы не забываем возвести в квадрат.
sin a = √1-(-1/4) = √1+1/4 = √5/4 = √5/2
sin(45°-a)=sin45°cosa-cos45°sina= √2/2*(-1/2)-√2/2*√5/2=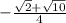 
Помним, что синус во второй четверти положительный.
Получаем ответ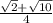 
Испытание состоит в том, что два раза подряд бросают игральный кубик.
Число исходов испытания
n=6·6=36
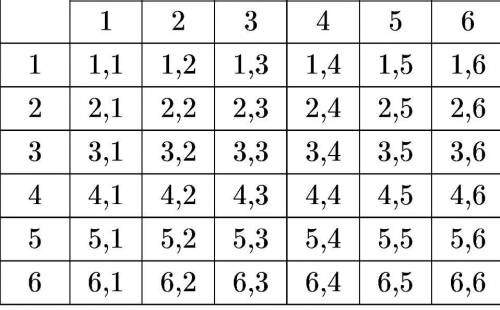
Результаты можно изобразить в виде таблицы:
( см. рис.1)
Первая цифра -число очков, выпавшее на первом кубике,
вторая цифра - число очков, выпавшее на первом кубике.
Получаем 36 двузначных чисел:
от 11 до 16; от 21 до 26; ... от 61 до 66.
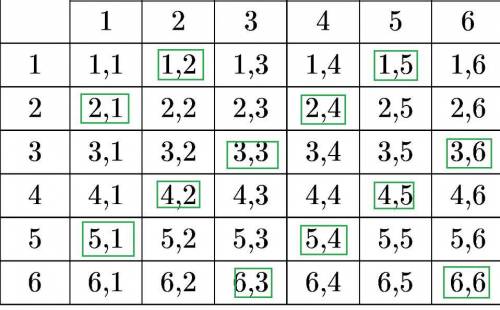
Событие A-"результатом двух последовательных бросков игрального кубика будет число, кратное трем"
m=12 ( cм. рис. 2)
это двузначные числа:
12;15; 21;24;33;36;42;45;51;54;63;66
По формуле классической вероятности
p(A)=m/n=12/36=1/3
